学びをいかそう わくわく算数ひろば 同じものに目をつけて 図を使って考えよう ②分数と小数・整数の関係 p168 1 p168 3 p169 5算数 「図に表すことで,100%や114%を捉えよう」 「図に表すことで,100%や114%を捉えよう」 ~量の大きさと割合の違いを明確にし,基準量・比較量・割合の関係を捉える~ B5 の結果を分析すると,示された割合を解釈して,基準量と比較量の関係を表している図を判断すること,また,身近な ものに置き換えた基準量と割合を基に,比較量に近いものを判断し・日常生活の中から、割合 関係にある事柄を見つ け、図や式などを用いて 数量の関係どうしを割 合で比べることができ る。 簡単な場合についての割合 ※本時 1/2 包帯の伸び具合を比べる場面において、二つの数量の関係 )

割合の3つの公式の覚え方と使い方 小学生に教えるための分かりやすい説明 数学fun
割合 関係 図 算数
割合 関係 図 算数-2 1 r学ぼう!算数』における同種の量の割合の指 導の流れ 次にr学ぼう!算数』の詳細な内容について分析 していく。図1と図 2はr学ぼう!算数』におけ る比・割合の導入場面である。 比の値を使うと,いろいろなことがわかるよう になります。学びをいかそう わくわく算数ひろば ④面積の単位の関係 下p14 1 下p15 2 下p21~22 1 下p23 3 下p24 1 下p25 1 ②がい数の計算 下p26~27 1 下p28 1 下p29 1 もとの数はいくつ 図をつかって




Lmnhgr8qowb0wm
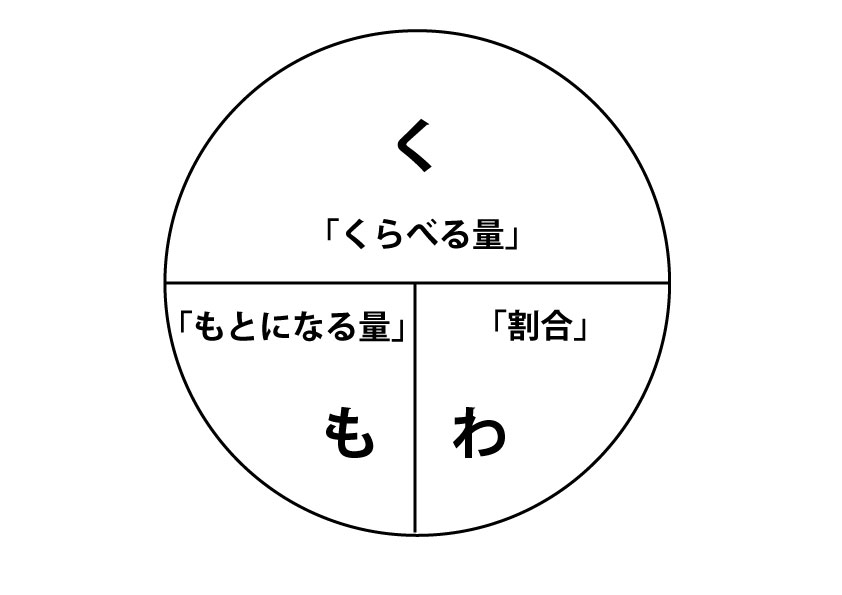
題意を関係図や線分図に表し ながら、数量の関係を捉え、全体 と部分、部分と部分の割合を求 める。 技 全体と部分、部分と部分 の割合を求めることがで きる。(ノート) 4 もとにする量と割合の 関係をつかみ,くらべる 量を求めることができ る。割合概念は,小学校算数の学習内容の中でも,児童にとって最も難しい内容の1つであろう。 図3:図が付された割合に関わる幾つかの問題 h28A8の正答率は745%であり,数値化を伴わない素朴な部分と全体の割合関係(及び割合小学校5年生の算数で習う『割合』は算数の中でも得意・不得意が顕著に分かれる単元です。 得意な子は公式をわざわざ覚えなくて もしくは、以下のそれぞれの頭文字をとって「く・も・わの図」でそれぞれの関係を導出するのもおすすめです。
者数の関係を考え、割合の意味を知る。 第2~4時 関係図や線分図を用いて、全体と部分の割 合や部分と部分の割合、比べる量、もとにす る量の求め方を理解する。 算数科 小学校 5年 「知識・技能」を定算数科 「C変化と関係『(2)異種の二つの量の割合』『 (3)割合』」における授業設計の視点 Ⅱ 「C 変化と関係『(3)割合』」 における基本的な捉え方 り入れる。このとき、全体と部分の関係、部分と部分の関係は、テープ図や数直線などの図、式を用い割合,比べる量の関係を捉えることができる 効果的な図についても考えた。それについて も合せて提案する。 2 子どもの苦手意識 具体的な場面で,割合の3 要素が捉えにく い理由について考察する。問題によって,比 べる量やもとにする量が変わるから
面積図:「わり算でも増える」がわかる! 面積図は、 「単位分数いくつ分か」 という考え方を身に付けるのに役立ちます。 また、わり算と聞くと減るイメージがあるのですが、 面積図を使うと増えるパターンについてもイメージしやすく なります。 具体的な使い方です。 まず、「 1 3 1 3 dLあたり 3 5 3 5 ㎡塗れる」を表しているのが左側の面積図です。 単位分数単元名 「割合」 算数科 小学校 5年 啓林館 「わくわく算数5下」 本単元の「割合」は、2つの数量があ るとき、一方が他方の何倍になっている かという関係を表す数であり、日常よく 使われている。 単元目標 割合で考えることのよさを知り、百分率そこで,乗法的オペレータ,つまり何倍という割合を表す図として関係図を用いることにしています。 乗法的オペレータ この関係図は,一方の量が他方の量の何倍になっているのかを矢印を使って簡単に図示したもので,第3学年から指導することにしています。 上の関係図は,青は赤の3倍,黄は青の2倍であることを表しています。 そしてこの図から,黄は赤の3




5年算数 割合の導入 実践報告その2 4マス関係図で進めていく ネコ好きな学校の先生の日常
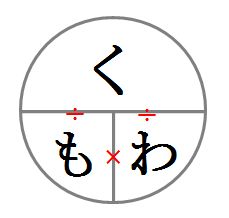



割合の基本を解説 割合の計算問題は算数というより国語の問題
小学生の算数 変化と関係・データの活用(数量関係) 練習問題プリント 無料ダウンロード・印刷 小学5年生の算数 割合(割合・比べる量・もとにする量の意味と求め方) 練習問題プリント お気に捉えさせていく。 (例)240人のうち、60人の割合は? ←線分図 4 ます表 ↓ 人数 60 240 割合 1 ② 線分図や表を使って、式を考えさせる 4つの数量を表した線分図や表に、数量の関係を見付けさせる。これら図表に関係を示す矢印関係図は、下のようになります 定価× =代金 だから =代金÷定価です 式 840÷10=07 答え07倍 割合は、百分率(ひゃくぶんりつ)で表すことがあります。百分率では、001倍のことを、1%(1パーセント)といいます。
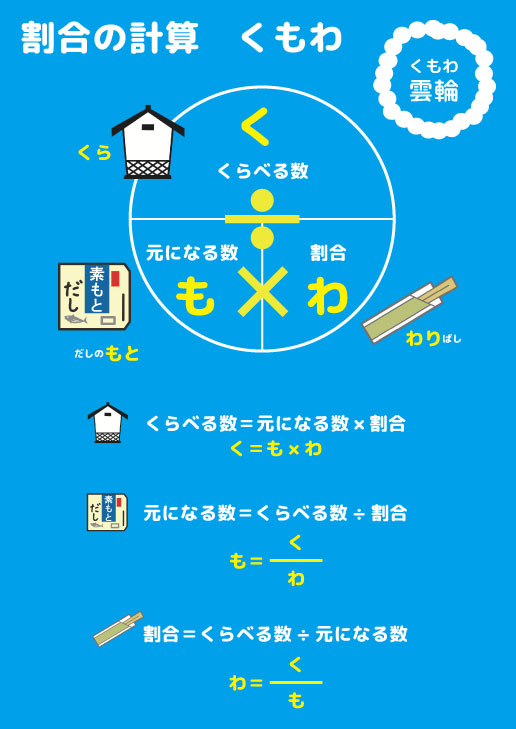



割合の計算方法をイメージで覚える 5年生の算数 算数検定7級




小5の難関 割合 をわからなくさせる3つの原因 算数コーチ Kazu
Likes, 0 Comments @flower298 on Instagram "算数*割合 くらべる量を求めていきました。 関係図がかければ楽々ですね。 ただ時々、どっちがもとにする量だっけ?となっている児童がいたので、繰り返し練習していきたいと思います。"本研究は,児童が苦手意識をもっている算数の 割合の学習において,学習者自身が動的なテープ 図を試行錯誤しながら主体的に操作することで, 数量関係のイメージ化が図られ,立式に結びつく ことの効果を検証するものであり,そのためにデ 比の問題(小6)「比と分数の関係③」 今日は、 比 (小6)のちょっとした問題をやってみましょう。 「比と分数の関係③」 では、問題をやてましょう。 のxの値を求めよ。 この問題は考え方2と比と分数によって解くことができます。 面積が72
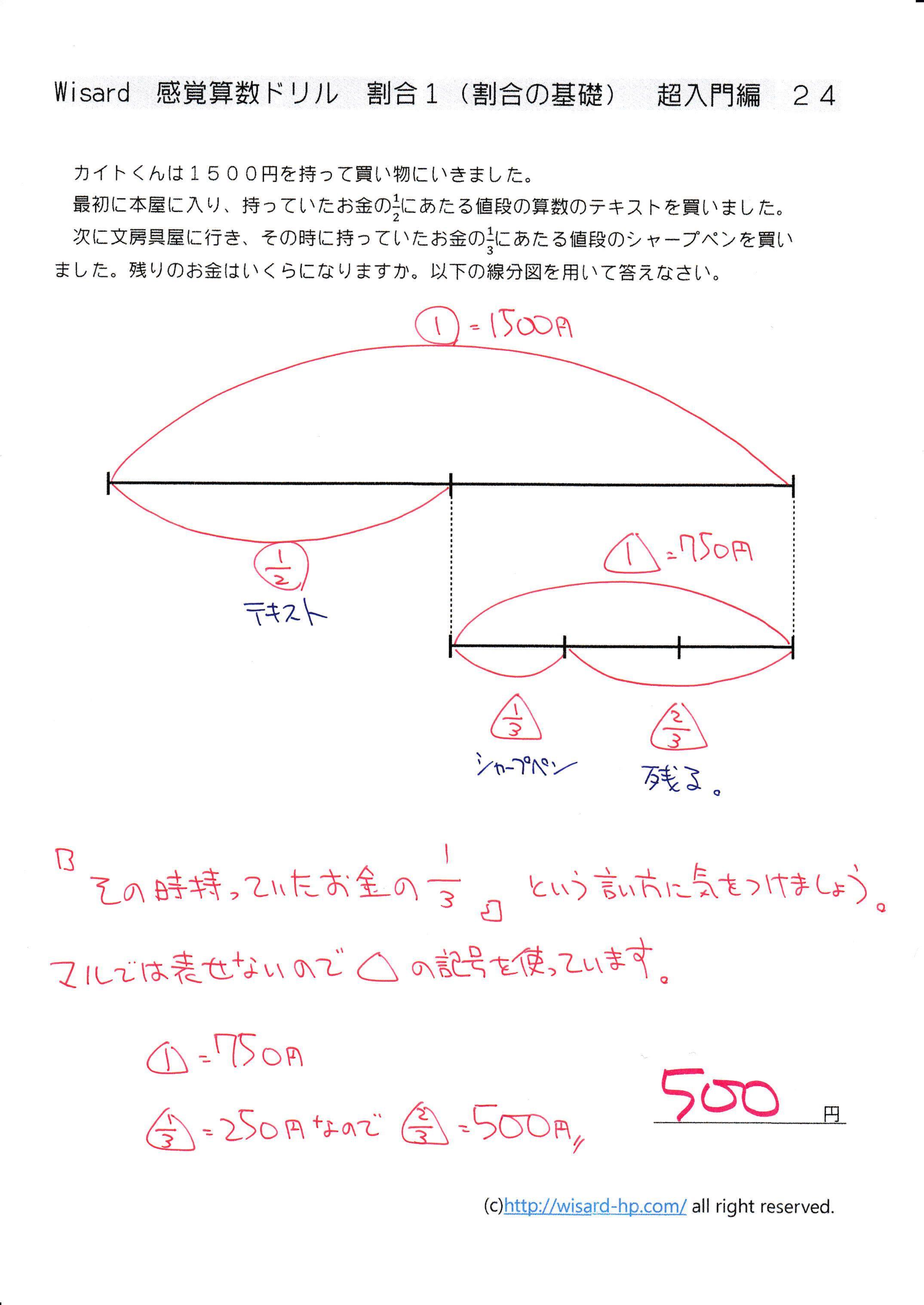



感覚算数ドリル 割合 入門編1 割合の基礎 Wisardnet 中学受験算数を攻略する教材サイト



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents S 053 Pdf
30 ÷ 100 = 03 そうです。 この公式では答えが『 小数 』になるのです。 そこで、上にある「もとになる量」「くらべる量」「割合」の関係の図をよく見てみましょう。 この答えを『%』に直したいとき: 100をかけてやればいいのです。 (100倍する視覚的に表現できる図を用いることが有効です。計算に用いる図には,加法と減法の線 分図や,乗法と除法の数直線,ブロック図, を使った図,十進位取り記数法のしくみ を図化したタイル図,分数の指導で用いる面積図などがあります。― 197 ― 割合の教授法に関する一考察 197 ・和田常雄のbb(ブラックボックス)図を利用した実践 倍とは、「ある量に働きかける操作の1つ」と考え、シェーマとしてブラックボックスを用いている。



5年算数 割合 2 円グラフ帯グラフの書き方



Www Pref Okayama Jp Uploaded Life Misc Pdf
第4学年 算数科学習指導案 平成27年11月25日 1 単元名 もとの数はいくつ 2 単元を貫くテーマ 単元を通して育てたい力は,「順にもどして解決する思考法を身につけること」である。算数割合文章題の課題分析と解法の過程 愛知教育大学心理学教室 多 鹿 秀 継 横浜国立大学 数学教室 石 田 淳 一 1。目的 算数文章題の解法過程は、一般に与えられた文 章を読んで理解し、理解した内容に基づいて問題 を解くことからなる(Hinsley、Hayes、&Simon、公式の丸暗記でいいの? 「割合」の学習というと、「公式」が頭に浮かぶ。 ① 「割合」=「比べられる量」÷「もとにする量」 ② 「比べられる量」=「もとにする量」×「割合」 ③ 「もとにする量」=「比べられる量」÷「割合」 という3つの「公式」である。 「割合」の学習では、この3つの「公式」を教え込み、そこに数値を当てはめて答えを導き出すと




感覚算数ドリル 割合 入門編1 割合の基礎 Wisardnet 中学受験算数を攻略する教材サイト




平成29年度 全国学力 学習状況調査 授業アイディア例 小学校 算数 国立教育政策研究所 National Institute For Educational Policy Research
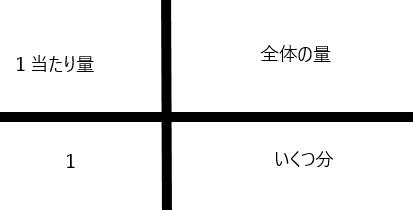
4マス関係表があると便利! 「単位量あたり」や「少数のかけ算・わり算」の文章問題になると、かけ算で求めるのかわり算で求めるのかわからなくなることがあります。 「1あたりを求めるならわり算! 」などのアドバイスをすることもありますが、そもそも文章問題の意味もわからなければ、あまり意味がないかなぁなんて思いながら指導することもあります 算数 小五 樋口万太郎 京都教育大学附属桃山小学校教諭 樋口万太郎 スッキリした分かりやすい構成で、子どもたちに伝わりやすい板書の書き方を目指す本シリーズ。 今回は「割合とその活用」の単元を使って、図の有用性に気づき、自分で図を使えるようになることを目指した実践を、 樋口万太郎先生(京都教育大学附属桃山小学校教諭)に解説していただき事件の謎を" 算数" で解き明かせ!ベテラン刑事ゼロと新米刑事イチが、" 算数"を駆使して、難事件に立ち向かう




中学受験 算数 割合 3つの公式を使って攻略 中学受験アンサー




くもわ の法則 小学算数 割合 の求め方にはこの 公式 が便利 Yattoke 小 中学生の学習サイト
図1 割合 につながる 素地的内容 と数学的 な見方 ,考え方 1年 大きい 数の計算 (何十 )±(何十 ) ちがいはいくつ 長さくらべ 5年算数「割合の導入」実践報告その1 今回は、実際に カルピス を題材に、割合を出すところまで進めていきます。 この割合を勉強するまで、「単位量」「速さ」の単元で 4マス関係図 を使って勉強してきました。5年算数 割合(1) わかる教え方のポイント 「割合」 は、ある量をもとにして、 くらべる量がもとにする量の何倍にあたるか を表した数です。 この勉強をわかりやすくするためには、 「線分図」 や 「関係図」 を使って 「割合の3つの用法」 をとらえさせたいと思います。 ①割合の意味と割合を求める問題の解き方 ②割合の考え方で比べる量を求める問題の解き



Www Kyoto Be Ne Jp Ed Center Tangensp 3syudata 5san Wariai Tanngenn1 Pdf




割合の3つの公式の覚え方と使い方 小学生に教えるための分かりやすい説明 数学fun
B:線分図や関係図で問題を整理し,全体の何倍(割合の積)になるかを考えて,問題を解くことができる。 A:上記に加えて,既習の「 01 倍の 02 倍は 01×02 = 002 倍の関係図」とつないで,全体の何倍(割合の積)になるかの考え方を見つけることが関係図の矢印の向きに気を付けるよう学習を重ねている。 第6学年算数科学習指導案 から比較量とするaに矢印が出され,比メーターを使って割合の関係図のようにも比の値を考えられるよ




Lmnhgr8qowb0wm



割合 線分図で倍 百分率 歩合がわかる 公式も くもわ も不要 みみずく戦略室




割合の3つの公式の覚え方と使い方 小学生に教えるための分かりやすい説明 数学fun
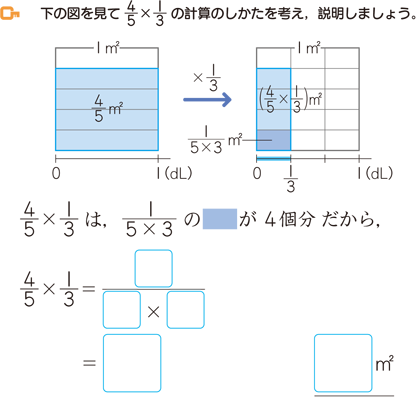



面積図 算数用語集
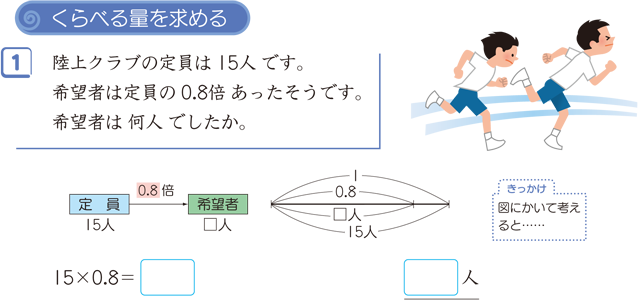



割合の3用法 算数用語集
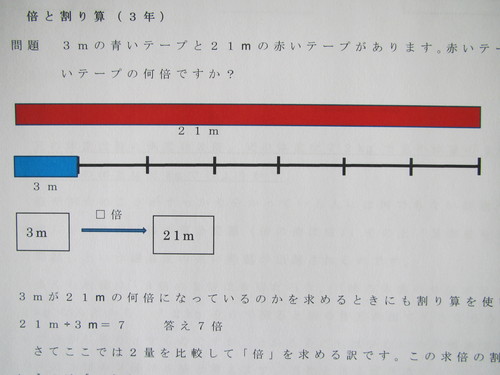



割合の本を出そう10続き 石原清貴の算数教育ブログ



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 5 512 Pdf




面積図の縦と横は何を表すのか かけ算の順序の昔話




学力テスト 割合 石原清貴の算数教育ブログ




Amazon Co Jp 算数 割合マスター タヌ様と漫画で学ぶ 基礎から中学受験まで 小学生の割合 線分図 食塩水 損益算 タヌ様の算数マスター Ebook 小山 秀人 中村夏子 本
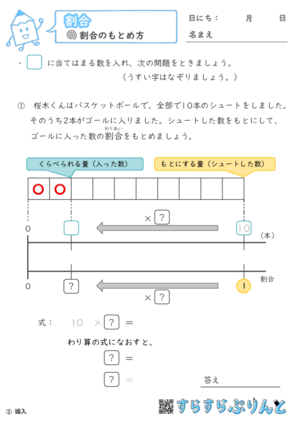



割合 割合の求め方 小学5年生算数 無料プリント教材



くもわ の法則 小学算数 割合 の求め方にはこの 公式 が便利 Yattoke 小 中学生の学習サイト



Www Pref Tochigi Lg Jp M03 Documents Sannsuu Pdf
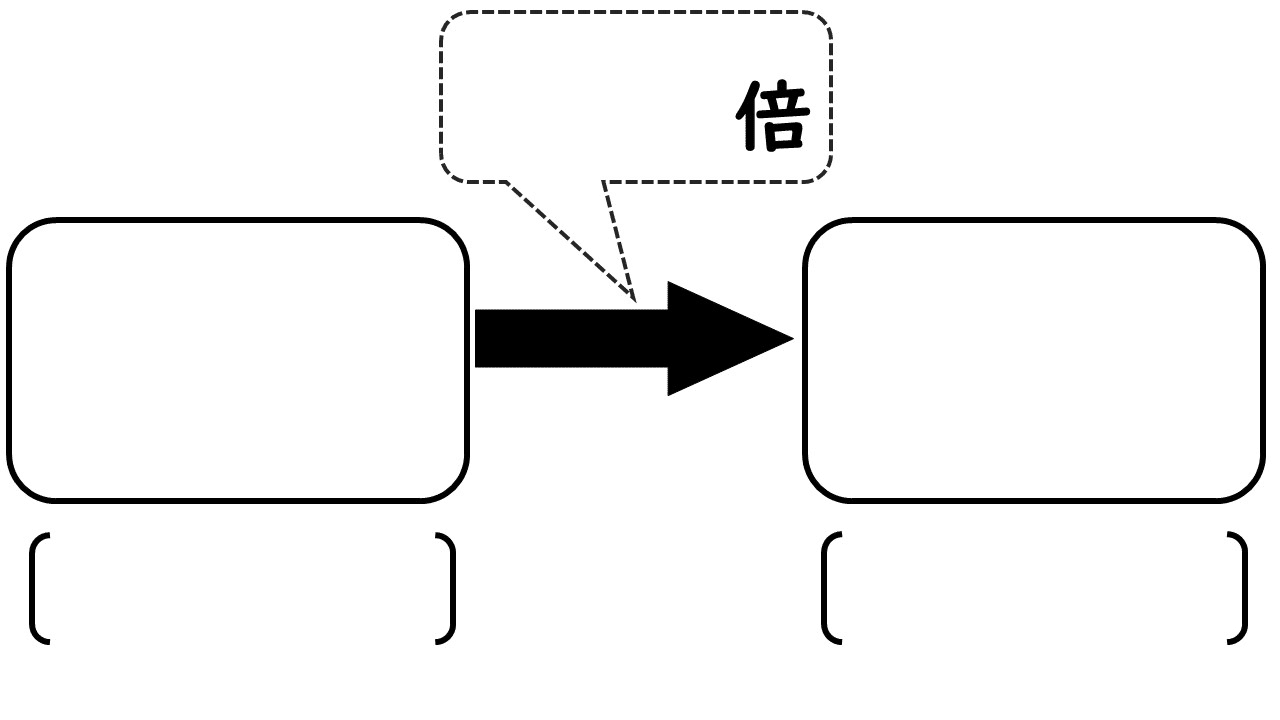



5年算数 割合 飛び込み授業 この関係図を使いこなせるようになると 文章問題もテンプレはめ込みで ある程度解けるようになってきます 図に落とし込む 転換 何が何倍で何になる を図式化したもの 清水智 Shimizu Satoshi 教育ict 学級経営コンサルタント



割合をどう教えるか1 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



小学5年生の割合のポイント 割合がこの図でわかる 解ける Tk科学教育オフィス




割合 とはなにか Z Square Z会



Http Park Saitama U Ac Jp Matsuzaki E7 A0 94 E7 B6 E5 Ae hp E5 86 99 E7 9c 9f E5 B9 B4 E5 Ba A6 E7 Ac Ac24 E5 9b 9e E6 95 B0 E5 Ad A6 E6 95 99 E8 B2 E5 Ad A6 E4 9a E5 E5 Ad A6 E9 99 E7 94 9f E7 Ad E7 99 Ba E8 A1 A8 E4 9a E6 A3 Ae E5 B6 8b E9 Ba 97 E5 A5 E6 9d Be E5 B5 9c E6 98 Ad E9 9b 84 Ef 80 Ef 80 8c E5 B2 E5 90 81 A8 E7 99 Be E5 86 E7 8e 87 81 Ab 81 81 84 81 A6 81 Ae E5 90 84 E7 Be E7 Ae 97 E6 95 B0 E7 91 E6 95 99 E7 91 E6 9b B8 81 Ae E6 Af 94 E8 E6 9c E8 A8 8e Ef 8d 80 8e E5 80 8d 80 8f 81 Ae E5 8f 96 E6 B1 81 84 81 Ab E7 9d 80 E7 9b Ae 81 97 81 A6 Ef 8d 80 8d Pdf



1



15 3月 15 悠閑荘望楼 教育についてかんがえる



5年算数 割合 2 円グラフ帯グラフの書き方




小5 算数 小5 53 帯グラフ 円グラフ Youtube



5年算数 割合 2 円グラフ帯グラフの書き方



Www Shinko Keirin Co Jp Keirinkan Sho Text Sansu File Sansu Pamphlet Chapter09 Pdf




割合の計算




割合 とはなにか Z Square Z会



Www Pref Tochigi Lg Jp M03 Documents Sannsuu Pdf



算数の時間 6年3組 宮崎市立東大宮小学校




基本から応用まで使える 割合の問題を解くときに役立つ 線分図 の考え方 中学受験ナビ




算数 これができれば大丈夫 きょうこ先生が解説 2 割合 速さ 場合の数編 親子で挑む 算数つまずき攻略法 朝日新聞edua



Www Pref Tottori Lg Jp Secure Nitinannkankeizu Pdf



6年算数分数 分数 教え方2
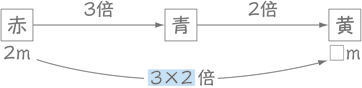



線分図と関係図 算数用語集



5年算数 割合 1 わかる教え方のポイント




5年 4マス関係表で 関係を見える化する 単位量や小数のかけ算 わり算に便利 ネコ好きな学校の先生の日常
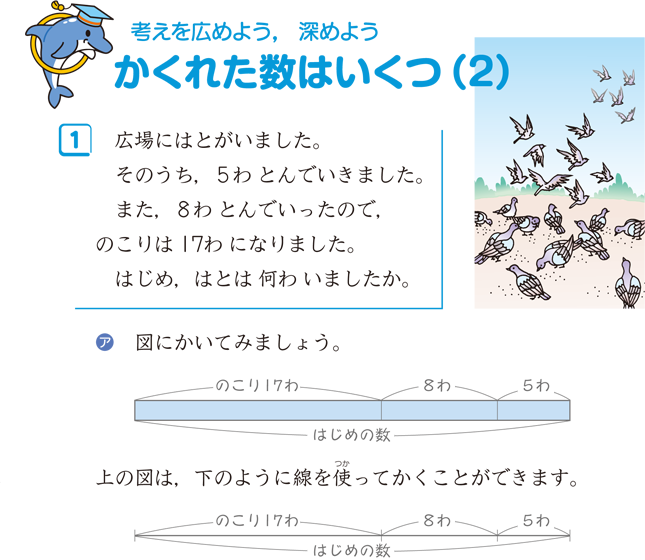



線分図と関係図 算数用語集



5年算数 割合 3 わかる教え方のポイント



1




小5 算数 公式を使わない 割合 講座 基本編 Youtube




くもわ の法則 小学算数 割合 の求め方にはこの 公式 が便利 Yattoke 小 中学生の学習サイト




新しい算数 2年度用 小学校教科書のご紹介 東京書籍




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




5年算数 割合の導入 実践報告その2 4マス関係図で進めていく ネコ好きな学校の先生の日常



5年算数 割合 3 わかる教え方のポイント



ハイレベル文章題2 線分図を利用する文章題



5年算数 割合 1 わかる教え方のポイント



3



テープ図説明器 ヒシエス誠文社 ヒシエス誠文社
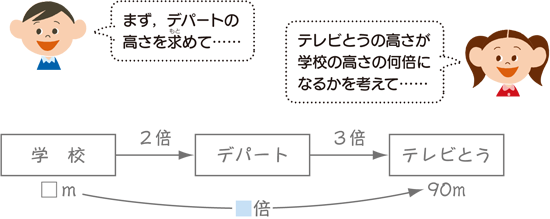



倍関係 算数用語集
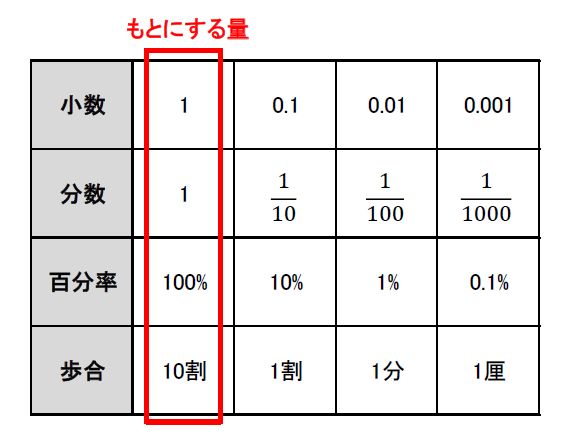



割合 線分図で倍 百分率 歩合がわかる 公式も くもわ も不要 みみずく戦略室



割合指導の第1 3時 教育考現学
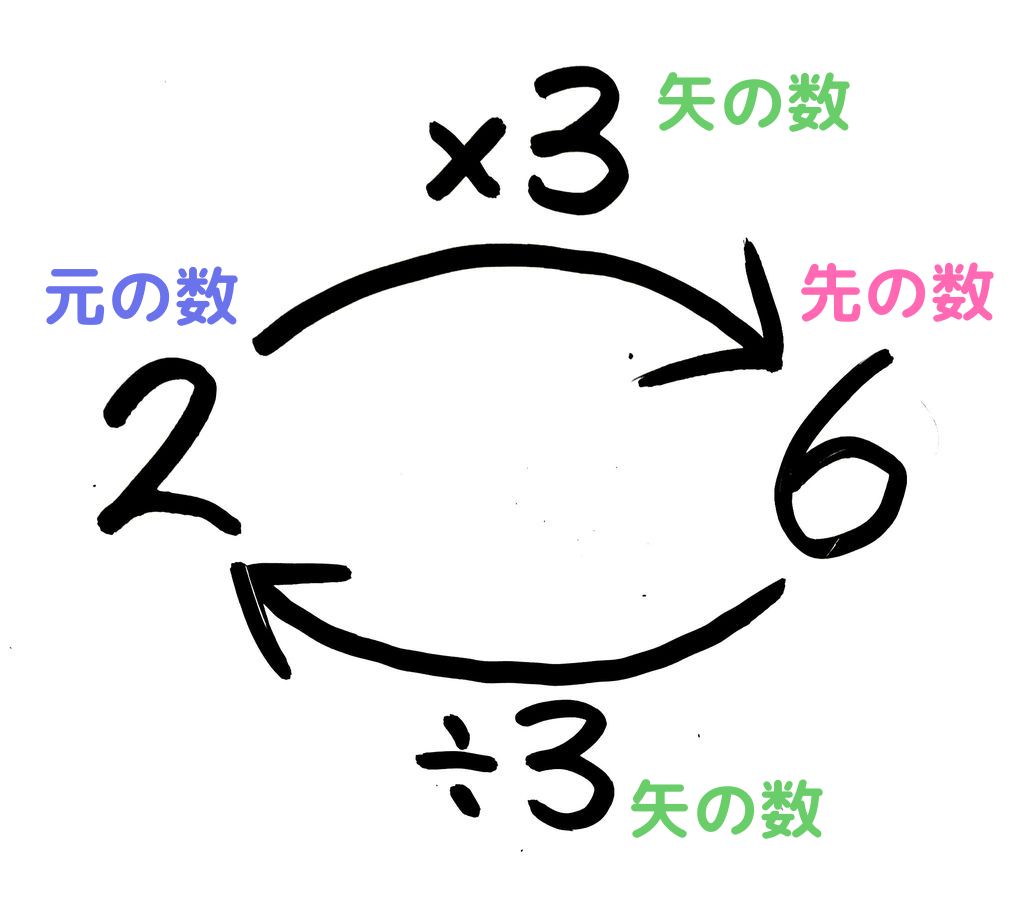



小学5年生 割合の簡単な求め方は くもわ 公式より分かりやすい出し方 そうちゃ式 分かりやすい図解算数 別館
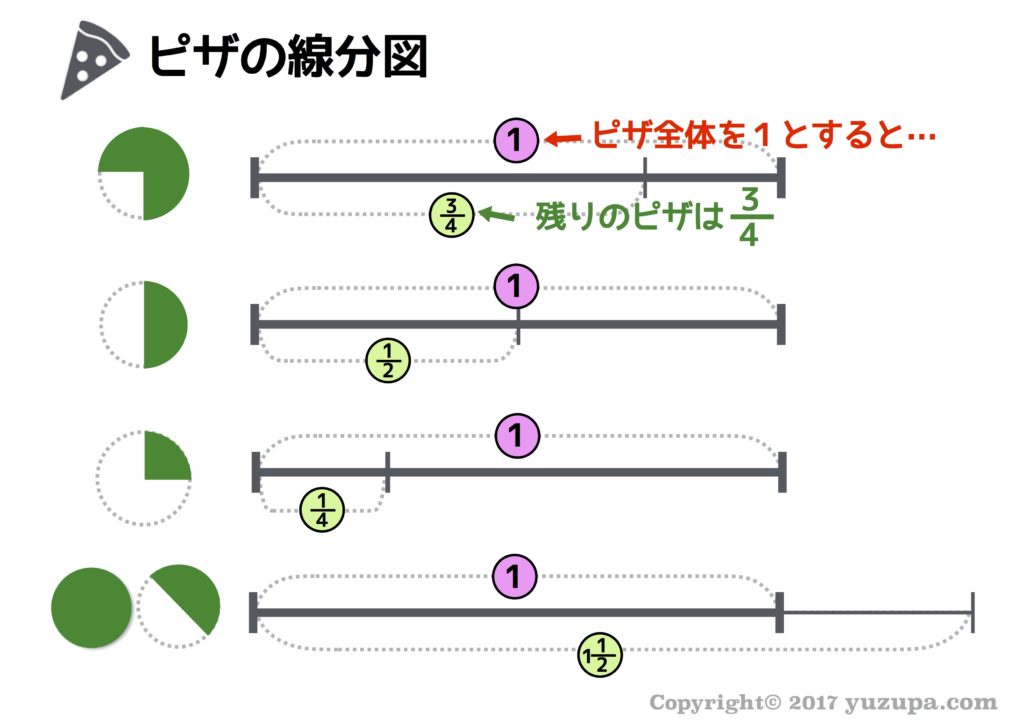



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋
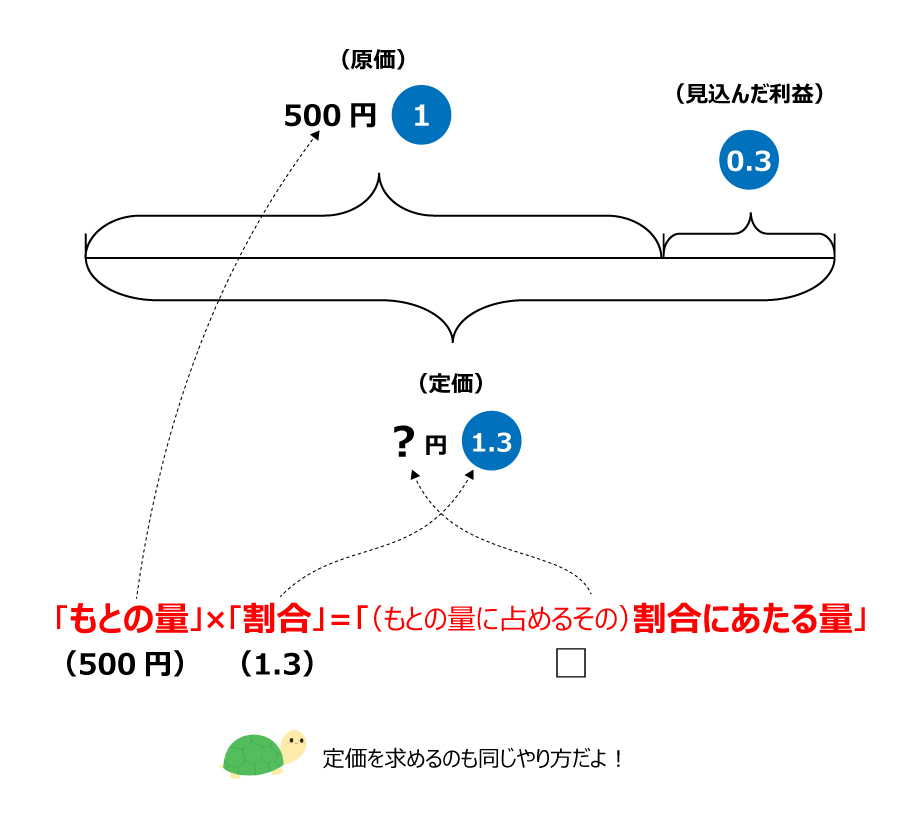



基本から応用まで使える 割合の問題を解くときに役立つ 線分図 の考え方 中学受験ナビ




小6算数 線分図を2本かく分数の割合 ブログ アビット




すきるまドリル 小学6年生 算数 比と比の値 比と比の利用 無料学習プリント すきるまドリル 無料学習プリント




5年算数 割合の導入 実践報告その2 4マス関係図で進めていく ネコ好きな学校の先生の日常




4マス関係表 深く息を吐く



比べて 全体と部分 部分と部分 割合とグラフ 間嶋哲先生 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




割合の計算




私の実践 私の工夫 算数 線分図や関係図などを使って 筋道立てて考える 啓林館




小6算数 分数 分数 数直線 面積図 関係図で攻略 動画 みんなの教育技術




小学6年生 算数 7月 分数と割合 分数と割合の応用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




5年算数 割合 のわかる教え方 いっちに算数 のブログ
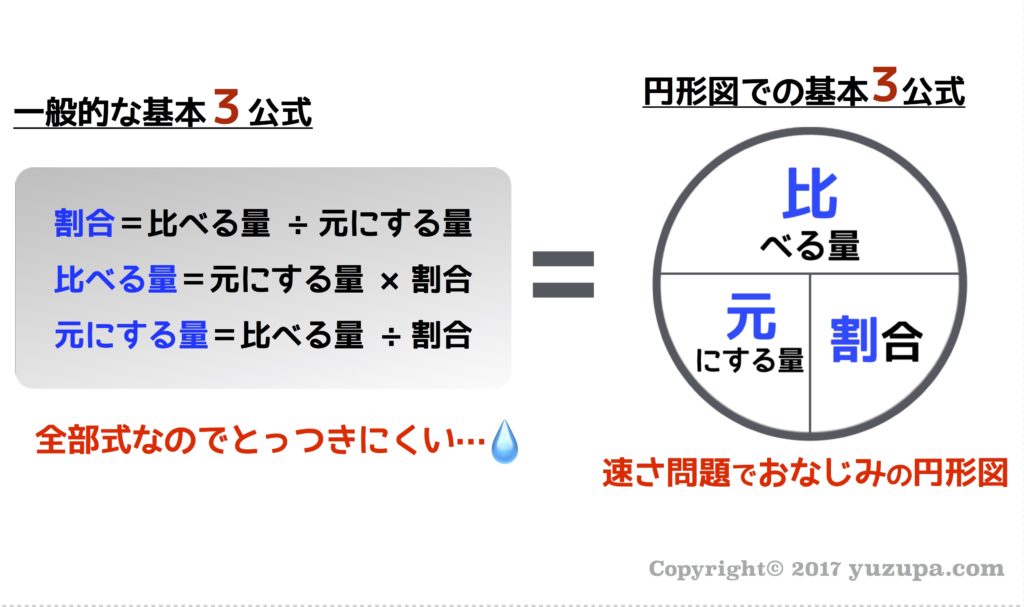



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋
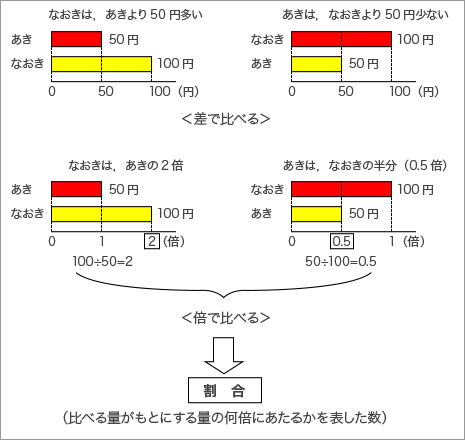



算数実践実例集 啓林館
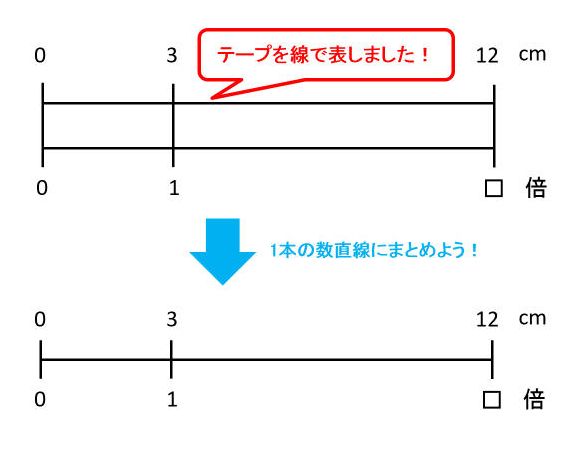



数直線を使いこなそう 目盛りつきの直線から線分図までを駆使して算数を攻略 中学受験ナビ



小学校6年生の算数問題です 割合を使って 全体を1とし 割合を考えてより Yahoo 知恵袋



1



ドリルズ 小学4年生 算数 の無料学習プリント倍と割合の問題



Http Www Hyogo C Ed Jp Gimu Bo Gakuryokutyousa Kadai H28 03 28a92 Pdf




割合の計算



Www Shinko Keirin Co Jp Keirinkan Sho Text Sansu File Sansu Pamphlet Chapter09 Pdf



Www Pref Okayama Jp Uploaded Life Misc Pdf
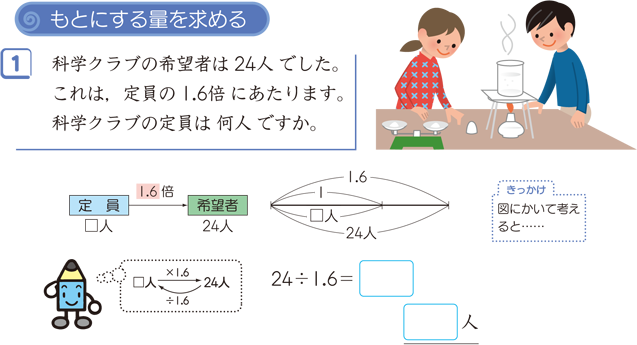



割合の3用法 算数用語集
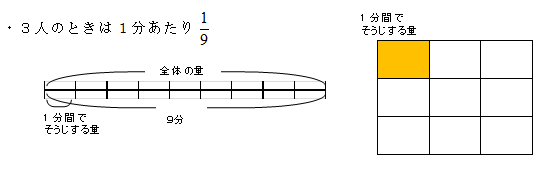



私の実践 私の工夫 算数 線分図や関係図などを使って 筋道立てて考える 啓林館



5年算数 割合 2 円グラフ帯グラフの書き方
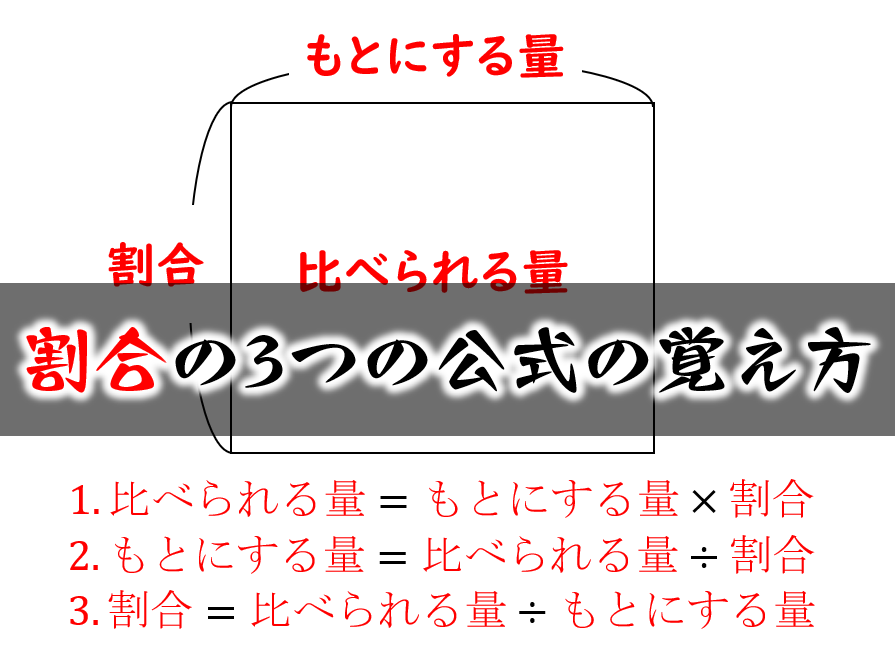



割合の3つの公式の覚え方と使い方 小学生に教えるための分かりやすい説明 数学fun




Amazon Co Jp 算数 割合マスター タヌ様と漫画で学ぶ 基礎から中学受験まで 小学生の割合 線分図 食塩水 損益算 タヌ様の算数マスター Ebook 小山 秀人 中村夏子 本
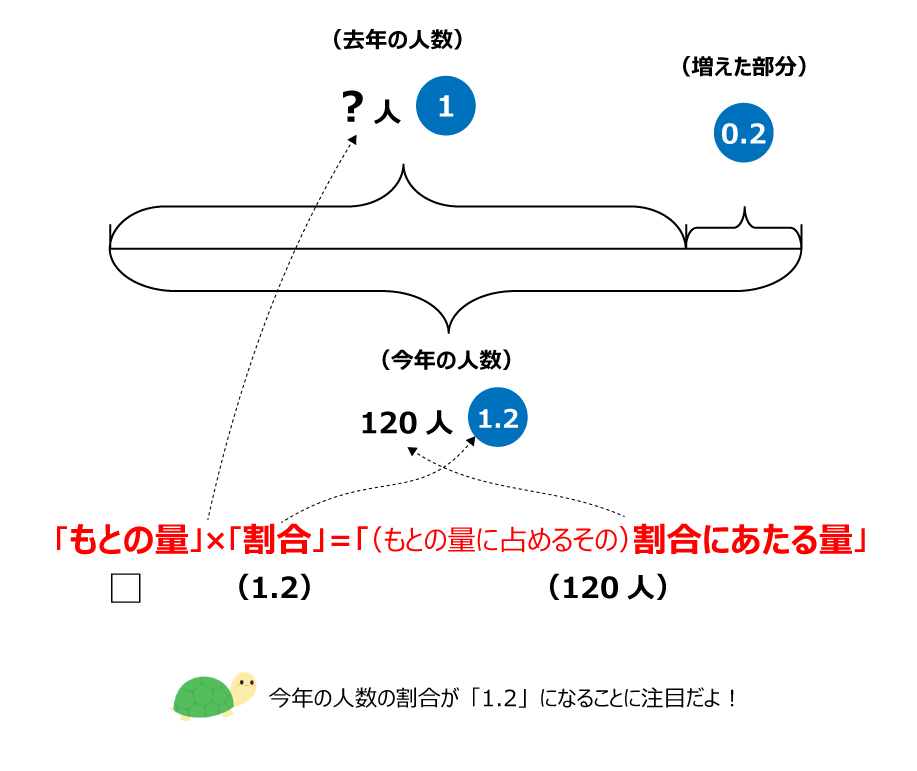



基本から応用まで使える 割合の問題を解くときに役立つ 線分図 の考え方 中学受験ナビ
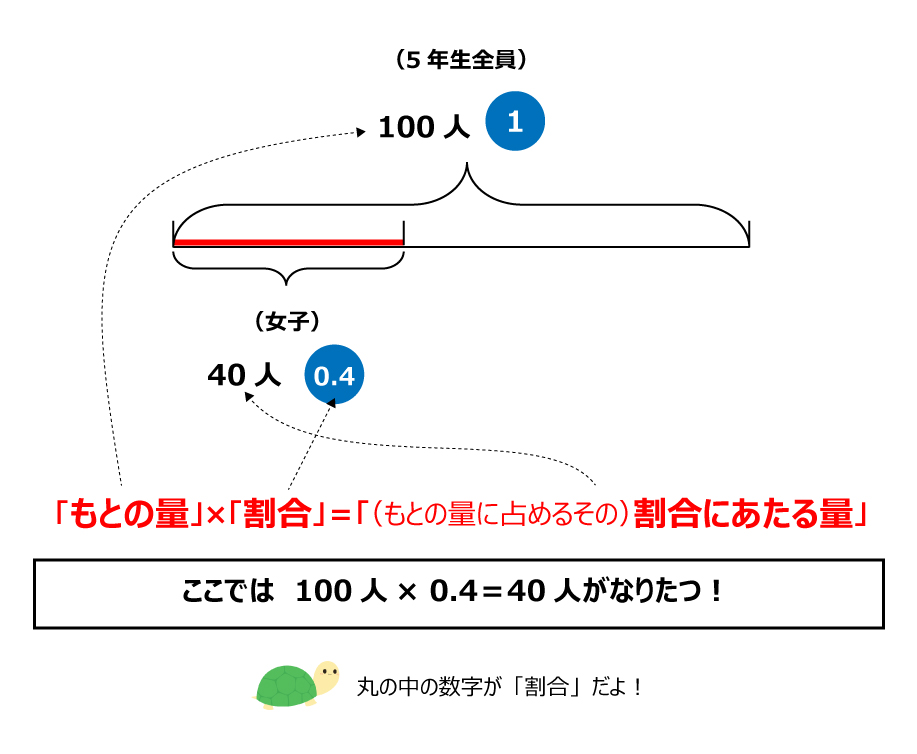



基本から応用まで使える 割合の問題を解くときに役立つ 線分図 の考え方 中学受験ナビ
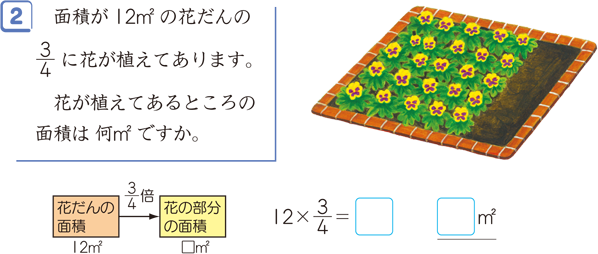



割合を表す分数 算数用語集




小学5年生の算数 5月 単位あたり量 人口密度 でシェーマ図を使いました 小学生ライフ 毎日の勉強と習い事の話




割合を表す 何倍か 塾の先生が作った本当に欲しいプリント 楽天ブログ
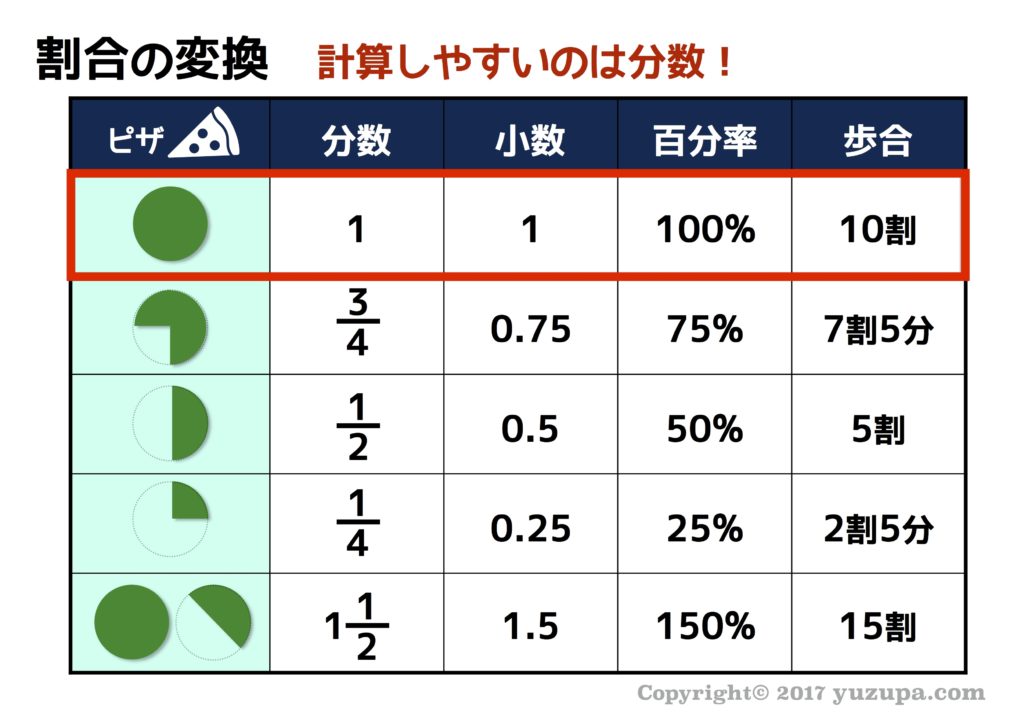



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




くもわの図 Youtube




算数 これができれば大丈夫 きょうこ先生が解説 2 割合 速さ 場合の数編 親子で挑む 算数つまずき攻略法 朝日新聞edua




わくわく算数忍者 7 割合修行編 割合のテストに強くなりたいキミへ の巻 学力ぐーんとあっぷシリーズ Amazon Com Books
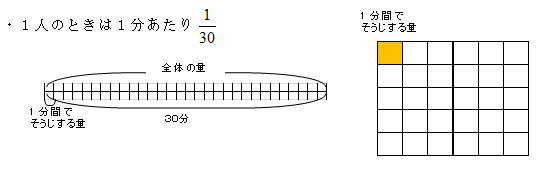



私の実践 私の工夫 算数 線分図や関係図などを使って 筋道立てて考える 啓林館
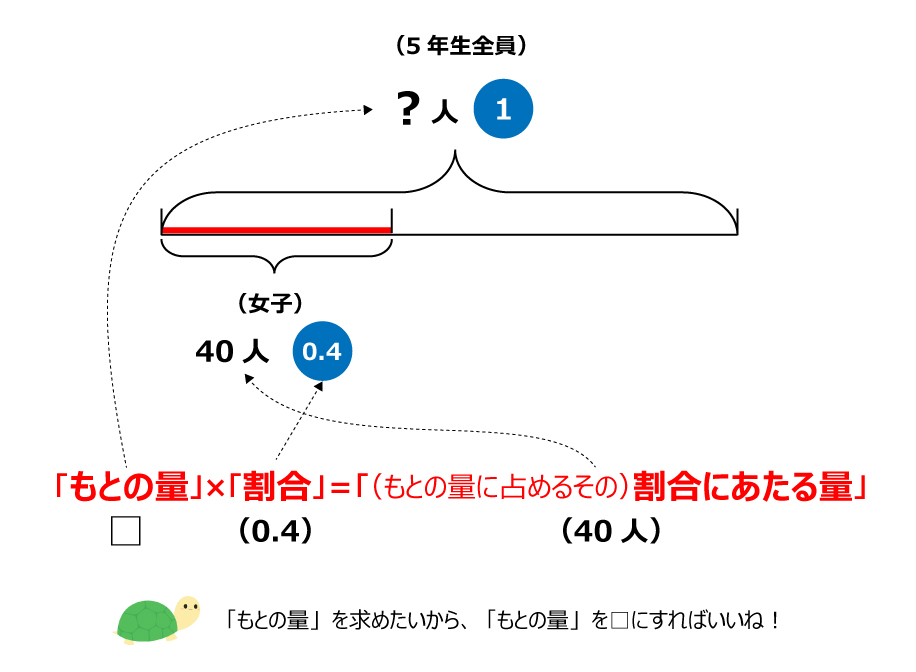



基本から応用まで使える 割合の問題を解くときに役立つ 線分図 の考え方 中学受験ナビ



0 件のコメント:
コメントを投稿