手がかりが少ない 2つの円の相似の中心oを、図示しなさい。 ので、生徒の学習 (対応する点が見つ 状況をみながら取 けみくい)場合 り組ませたい。 対応する点の決め 方で、様々な解法 を見いだすことが できる。 2つの中心を通る中心線上に、相似の相似の中心に関するものです。 図2-1と同じ記号の下 bf とce df とae bh とcg dh とag これらは平行である 「図2-7 今までの図においてr は pq を円p の半径と円q の半径の比に外分した点でした。 5外接円の中心のことを外心というので 高校生の方は、しっかりと覚えておきましょう。 図形の角頂点と、外接円の中心を線で結ぶと それぞれの線は、外接円の半径になっている ので 長さがすべて等し
放物線の相似性
円 相似の中心
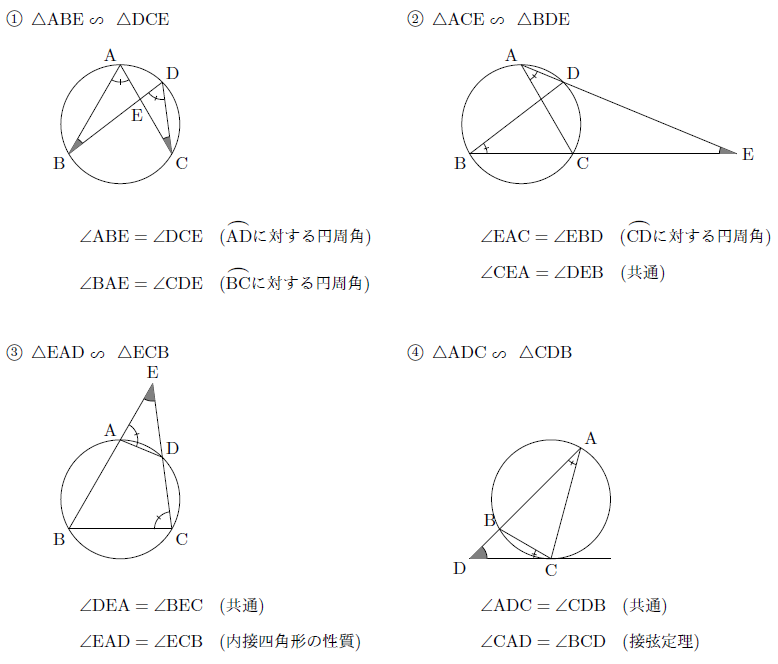
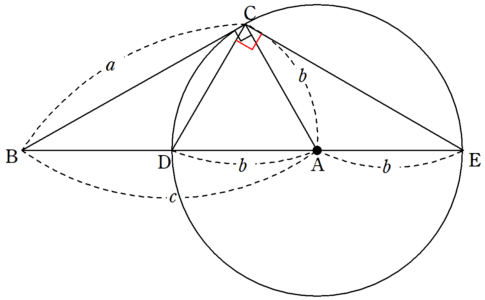
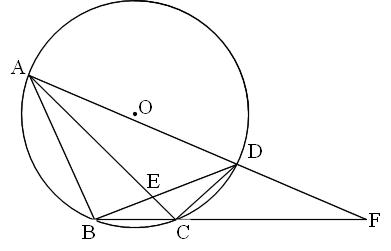
円 相似の中心-とwとは共円である。4つの円の中心のうち3つずつを頂点とする4つの三角形は完全四辺形 のつくる4つの三角形とwを相似回転の中心として直接に相似である。 補助定理2 円に内接する四角形の4つの頂点のうち3つずつのつくる三角形の垂心4つで4-1.平面図形 相似の証明 複合問題ほか 02年度出題 問1 図のように,円oに内接する abcがあります。円の中心oから辺bcに垂線をひき,辺bcとの交点をdとします。 odの延長と,点bにおける円oの接線との交点をeとします。次の問いに答えなさい。



Www Rimse Or Jp Research Past Pdf 8th Work06 Pdf
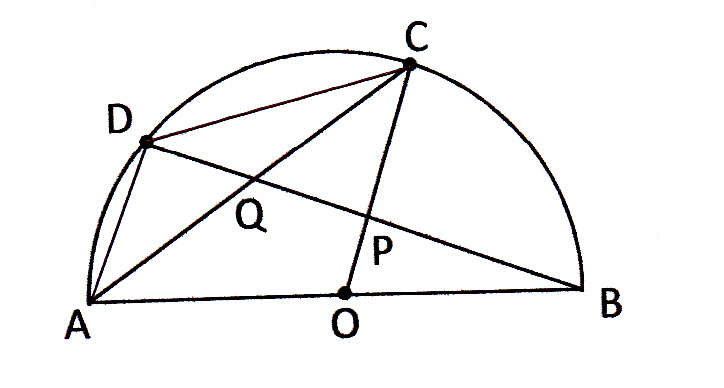
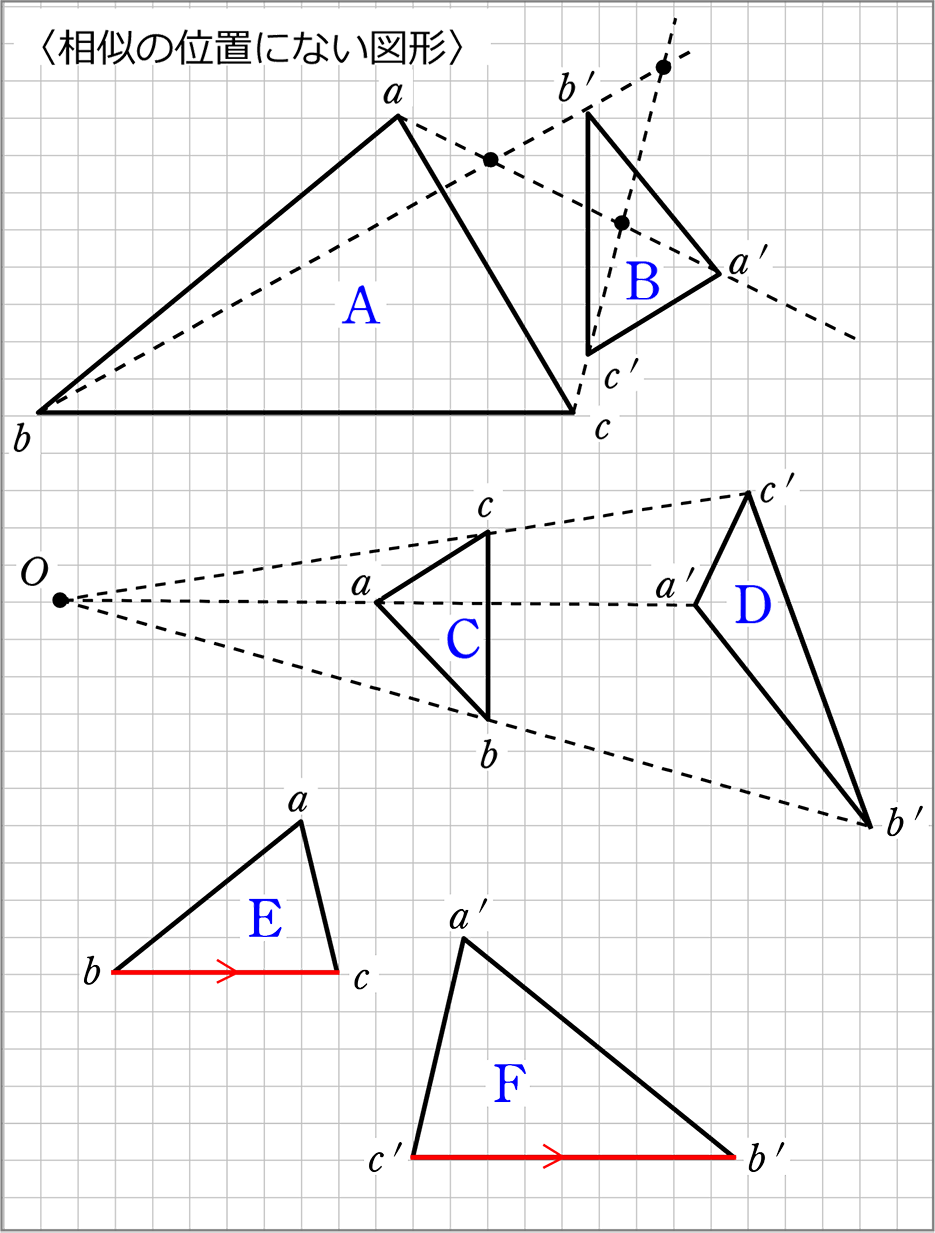
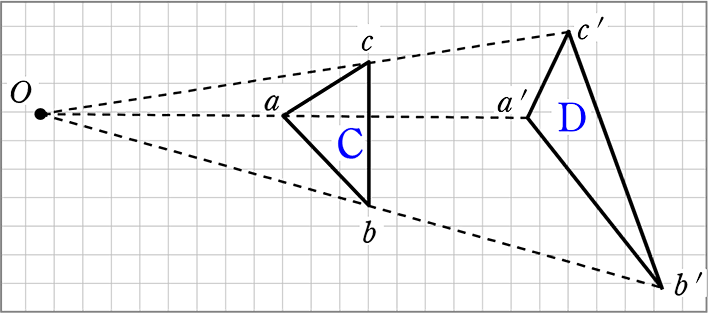
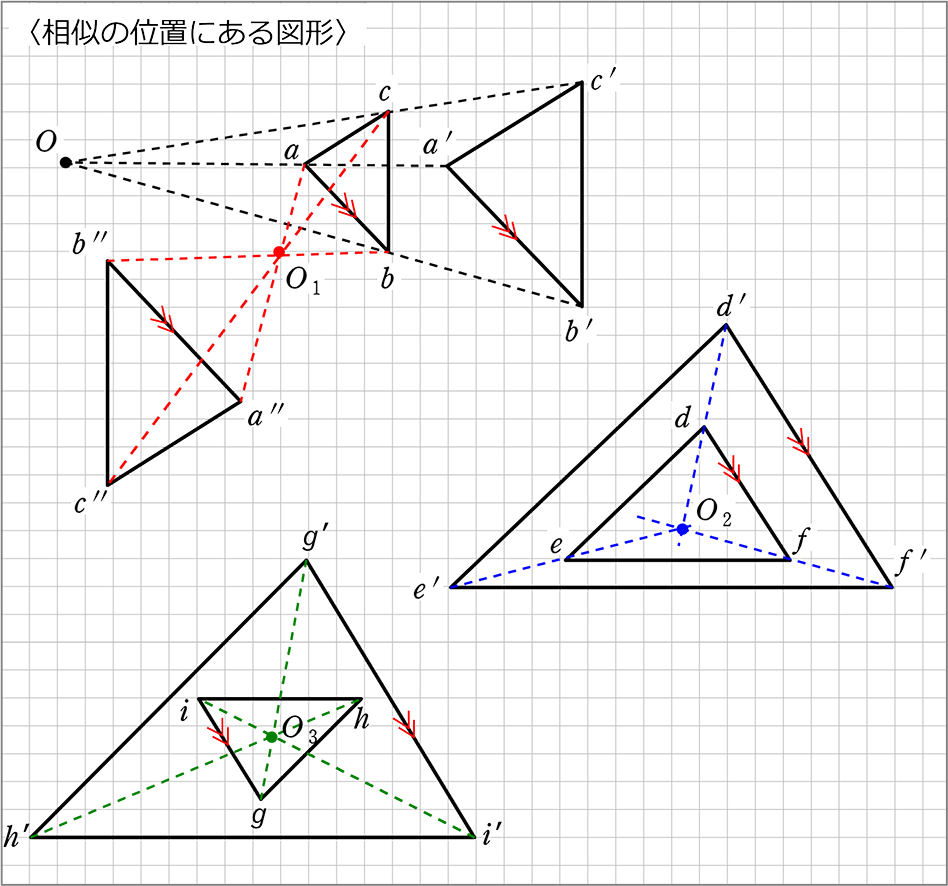
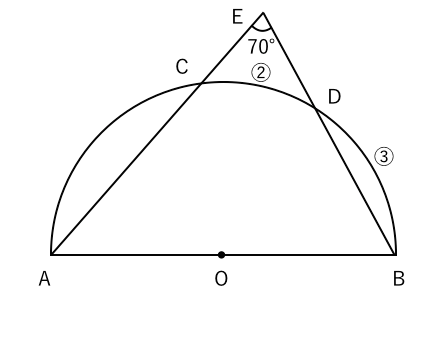
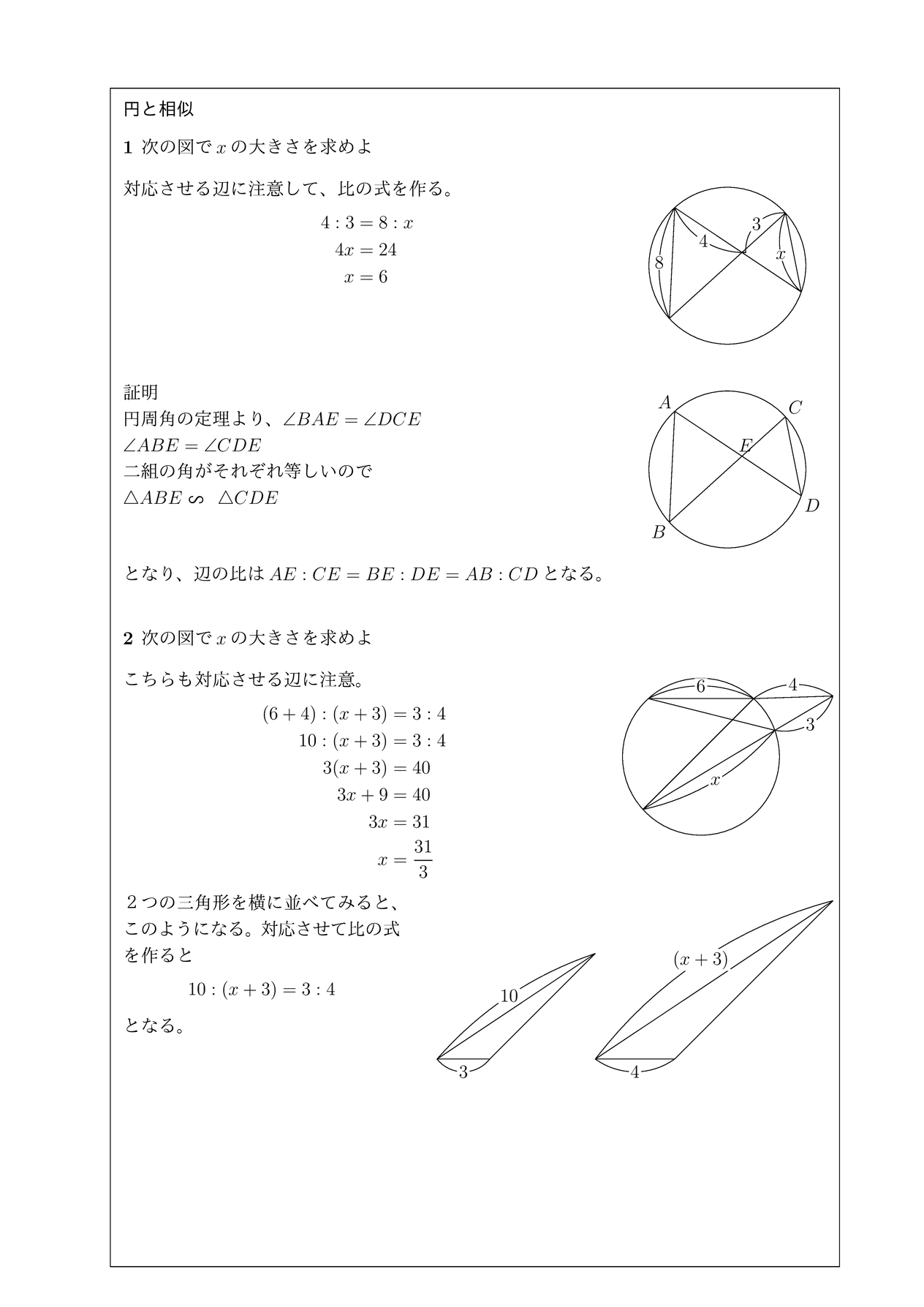
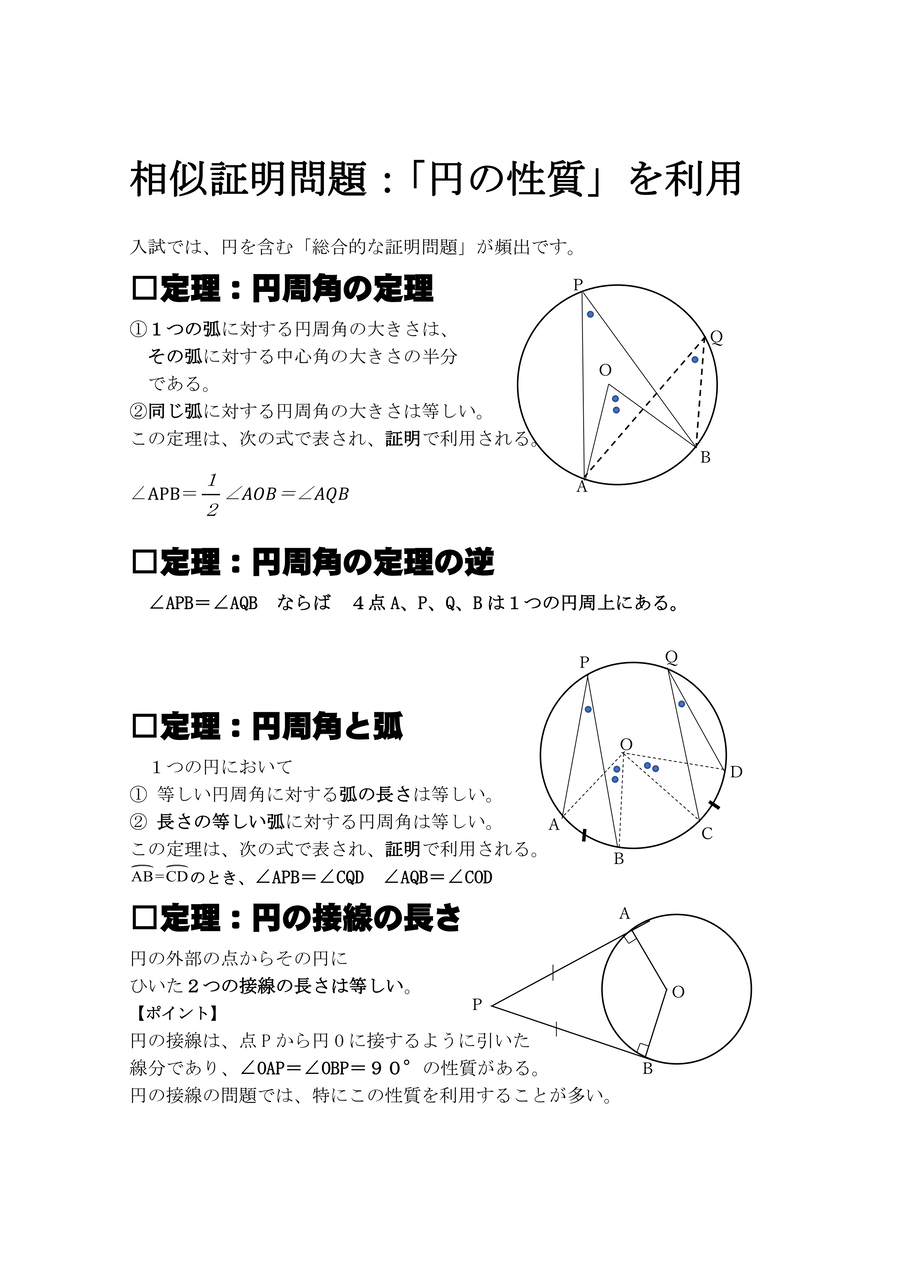
右の図のような円があり,異なる3点 a, b, c は円周上の点である。線分 ac 上に,2点 a, c と異なる点 d をとる。また,2点 b, d を通る直線と円との交点のうち,点 b と異なる点を e とする。 ∠ abe=35°, ∠ cde=80° であるとき, ∠ bec の大きさは何度か。 2つの図形の対応する点どうしを通る直線が 全て1点に集まり、 その点から対応する点までの距離の比が全て等しいとき それらの図形は、その点を相似の中心として、 相似の位置にある とN は相似の中心となる。 n を通る直線 g と円 o の交点を a,b,対応する円 o' 上の点を a',b' とする。4 点 t,t',a,b' および t,t',a',b はそれぞれ同一円周上にある。
まず点 o を円の中心とする、円周を考えます。 円周上の異なる位置にあるふたつの点 a, b と、点 o をそれぞれ結んだ半径のライン、つまりふたつの半径 oa と ob とで円を切って分けたとき、弧 ab と半径 oa と ob とで囲まれた図形を扇形といいます。 この記事を読むことで,すべての放物線が相似であることに納得できるでしょう。 まずは三角形の相似を考えることで,相似の位置と相似の中心について説明していく。 点Oから A B C の3つの頂点までの距離を3倍にした点をそれぞれP, Q, Rとする。3点P, Q, R別の三角形の相似に気づければ、計算はかなり楽になります。 下図の緑と水色の三角形の相似です。もちろん \(2\) つの角から相似とわかります。 青丸の角は、平行線の同位角です。 \(FD=6cm\) は、ピラミッド相似からわかります。 対応する辺の比は等しいの
2つの円の位置関係 2つの円の位置関係は5通り あり,中心間の距離と半径によって状況が変わってくるのでどのパターンなのか把握することが重要です。このページでは5通りの分類,交点,接線,相似の中心について整理します。 → 2つの円の位置関係2つの円の両方ともに接する円のことを共通接線と言います。 5つのパターンについて,共通接線の本数は順番に0本,1本,2本,3本,4本となります。 共通接線の本数は1本ずつ増えていくのがおもしろいです。 ちなみに,2つの円の交点の個数は 円の中心を作図する方法を思い出してもらえれば、edが直径になる理由がわかりやすくなるかなと思います。(2つの直径の交点→円の中心) ④ 弧bdの円周角 aeを引くと、 弧bdの円周角として∠bad=∠bedになりますね。



中3の数学です 円の縮図の書き方がわかりません 点oを相似の中心 Yahoo 知恵袋
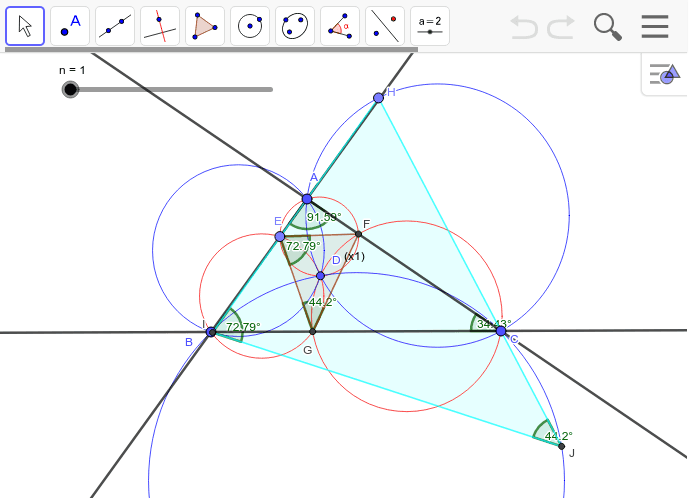



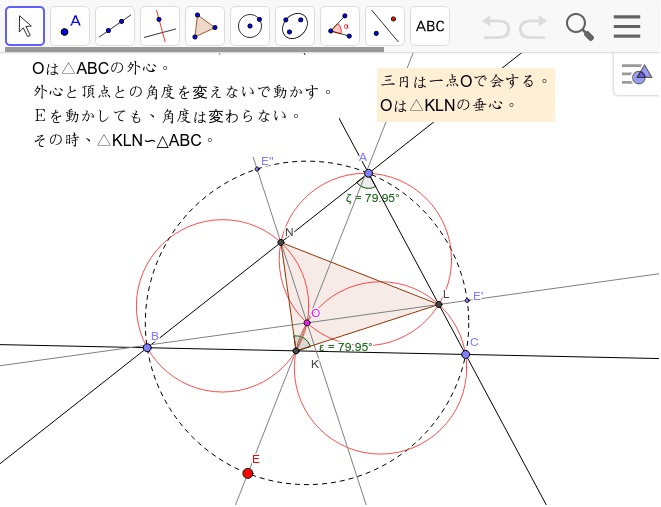
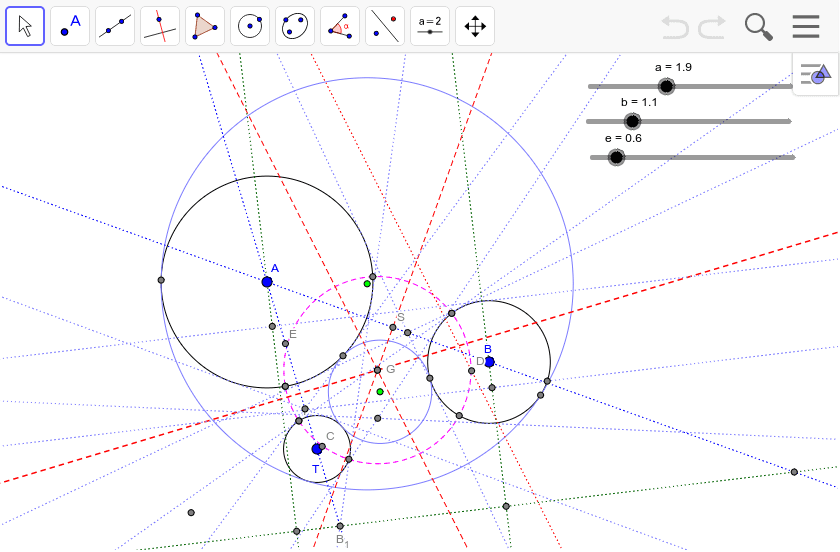
心を中心とする三円 Geogebra
証明パターン2 「中心oが∠apbの内部にある」 さあ、サクサク行くぞ。 つぎは、 中心Oが円周角の内部におさまってる形 だ。 補助線を緑で引いていくぞ。 点Pと中心Oを結び延長して、交点をqとしよう。 中心を通るから、PQは円Oの直径ってことになるね。相似な図形 拡大・縮小と相似 円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) この作図のためには、頂点を通る3円が一点で会することが重要な意味を持つ。 それらの三角形は全て相似であり、 その相似三角形がどのような三角形になるのかは、 3円が会する点(中心)の位置による。 それを探ってみよう。
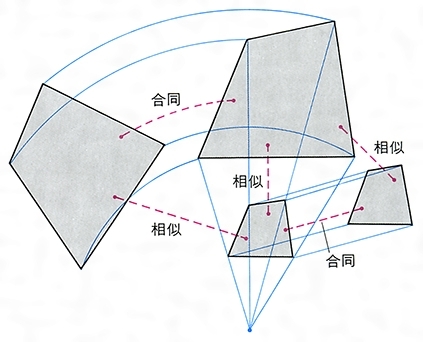



相似 数学 とは コトバンク




これらの相似の証明の仕方が分かりません 解き方を教えてください 出来れば 相似の証明 Clear
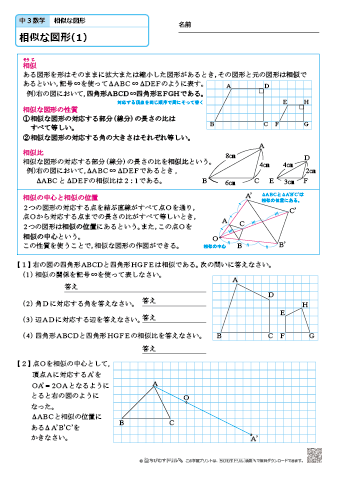
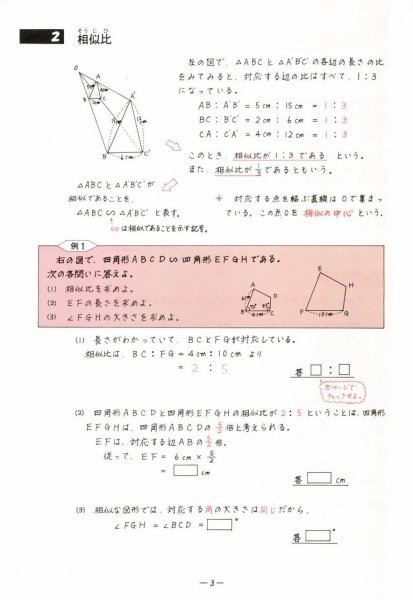
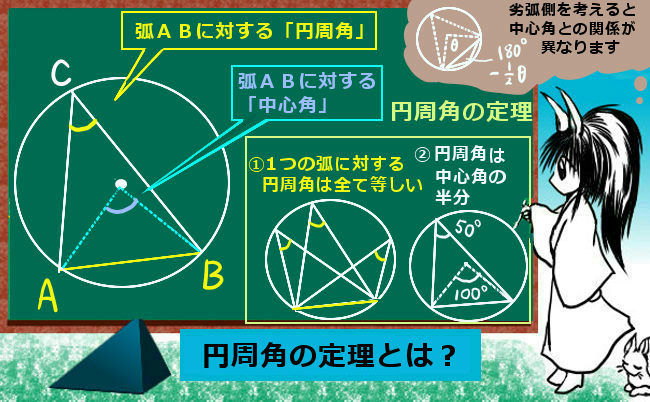
中心がoである円を円oと呼ぶ。円oにおいて、円周上の2点a , bをとったとき、aからbまでの円周の部分を 弧ab (こab)といい、 と書く。 を弧abに対する 中心角(ちゅうしんかく) という。また、弧abを中心角 に対する弧(こ)という。 円oの周上の点で、弧ab上にはない点pをとったとき、 を相似の位置 ここから,数回相似変換を中心に扱います.相似は平面図形の中で, 豊富な内容を含む分野の一つです.しかし,案外扱いづらく, 中学生,高校生に相似に関する出題をすると,合同の問題に比べて 極端にできなくなります.また,相似は図形に対する洞察力を調べるのに6章 相似 相似な図形 相似な図形とは?中学3年数学 相似比と辺の比中学3年数学 相似の位置と中心中3数学 相似な図形や中心の作図中3数学 三角形の相似条件中3数学 相似な三角形の辺の比中3数学 21相似の証明



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
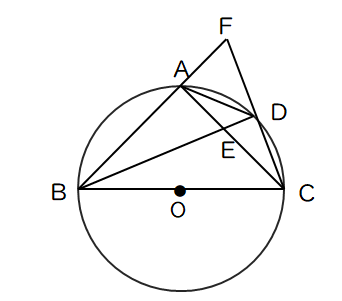
相似の中心は,2円の中心を 半径の比に内分した点,外分した点と2点あります. もし2円に共通外接線,共通内接線が が引ければ,交点が相似の位置の位置の中心です. この問題では共通外接線が引けるので, その点を相似の中心として考えましょう.Anm、 bln、 cmlの外接円の中心をそれぞれ、p、q、rとする。 (1) PQR∽ ABC (2) PQRが最も小さくなるとき、 PQRと ABCの相似比は:1:2である。 ゆえに、 O O を中心とする A,B,C A, B, C を通る円が存在する。 垂直二等分線の交点 = 中心 (外心) 三角形の三辺の垂直二等分線の交点は、 外接円 の中心である。 この中心を 外心 という。 証明 ABC A B C の辺 AB A B の中点を M AB M A B とし、 辺 BC B C の中点を M



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




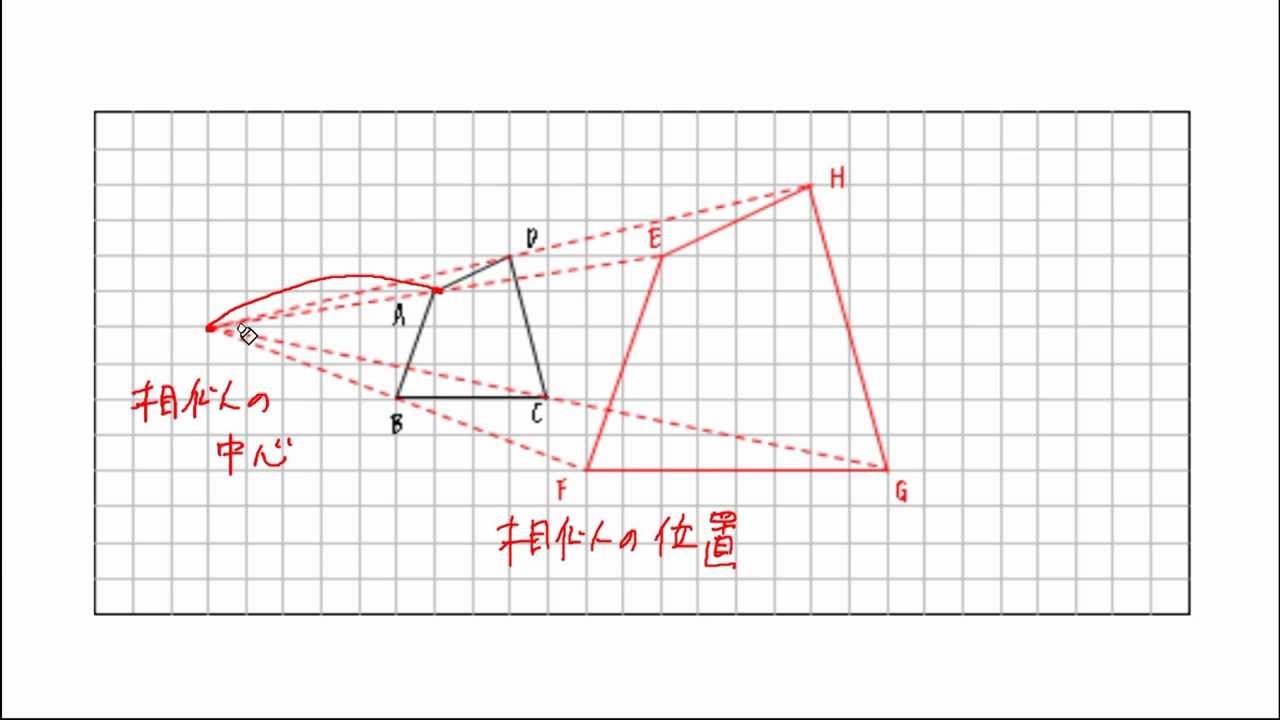
簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
次に、中心角について解説していきます。 中心角を一言で言うと、円周角の中心バージョンです。 円周角では、点を円周上に3つ置きましたが、円周上に2つ置いた点と、円の中心をそれぞれ結んだときに出来た角を中心角といいます。 これを図にすると、に中心となる考えの「相似の中心」はどこなのか、そして「相似の中心」とは 3 任意の中心と半径で円を描くこと 4 すべての直角は互いに等しいこと 5 直線が 2 直線と交わるとき、同じ側の内角の和が 180 度曑満である交わる2円・4点を通る円 類題1 類題2 類題・シュタイナー点 交わる2円と接線・4点を通る円 3円と共通弦 3つの等円 類題 2つの円と相似の中心 類題 アルベーロスの問題 丸山良寛の定理
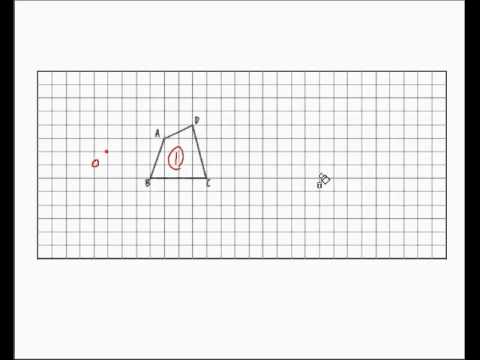



相似の中心と作図 Youtube




相似 算数 数学 英語塾のフェルマータ
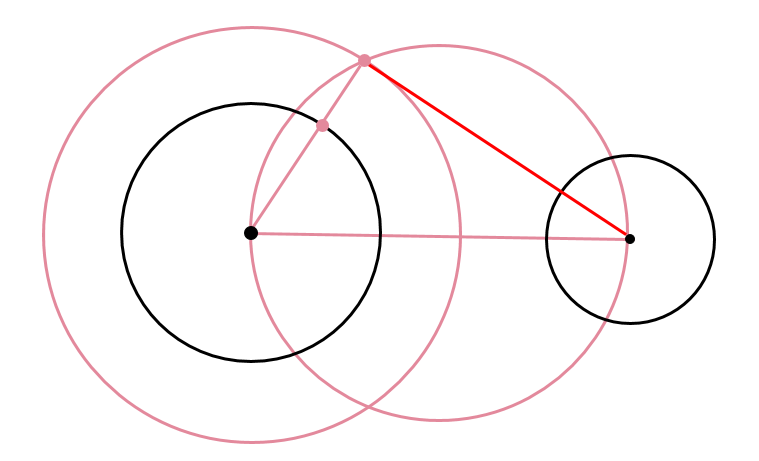
円oを pabの外接円とすると、op = oa = obである 円o'を qabの外接円とすると、o'q = o'a = o'bである oabと ao'bにおいて ∠aob = ∠ao'b (仮定より∠p=∠q、ともにその中心角) oabは二等辺三角形 (oa = obより) o'abも二等辺三角形 (o'a = o'bより) 前回の記事の最後に引き続いて, 相似変換 (中心相似) の応用を少しやってみる定円 内に定点 をとり, を通る弦 を引いて とせよ, という作図問題を考えてみる作図の解析をするために, 条件をみたす弦 が引けたと考えると, を相似の中心として, , であるから, は円 の周上の点でもある2つの円の相似の中心 W、P、Zは相似の中心で一直線上に並ぶ。 これを相似軸という。 他に3本ある。 Gは根心。 この軸と根心を用いて、アポロニウスの問題を解くことができる。



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3012 Pdf



平面の変換
円周角の定理の証明には ① 「円周角 ∠ A P B の内側」に円の中心 O がある ② 「円周角 ∠ A P B の線分上」に円の中心 O がある ③ 「円周角 ∠ A P B の外側」に円の中心 O がある の3つのパターンの証明が必要です。 このページでは、円周角の定理の証明『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので円の中心の作図方法 まとめ お疲れ様でした! 円の中心の作図は全然難しいものではありませんでしたね。 中心は、円周上のどの点からも等しい距離にある。 垂直二等分線を利用すると、2点から等しい距離にある点が作図できる。



円と相似 まなびの学園



三角形に内接する相似三角形 Geogebra
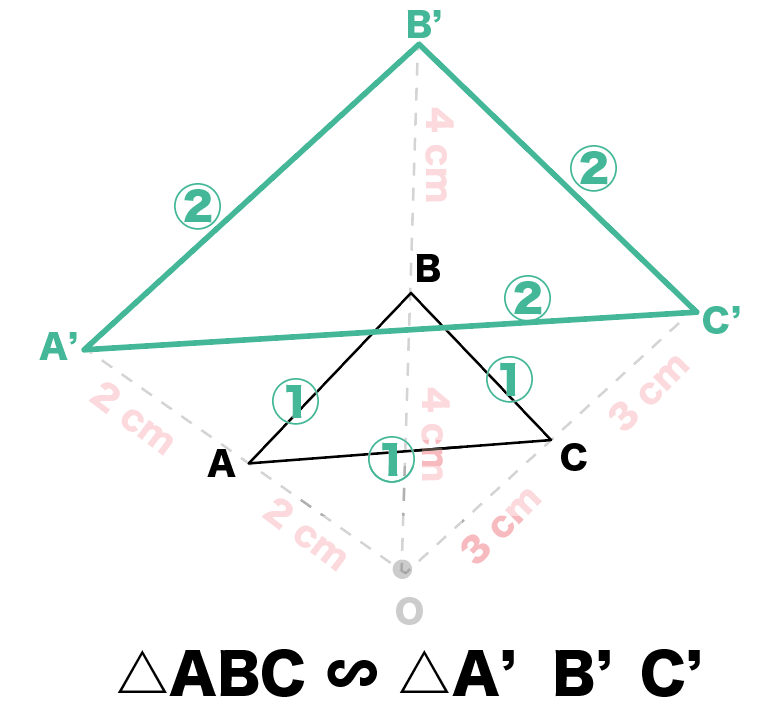
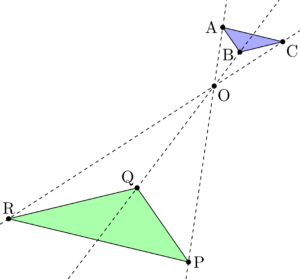
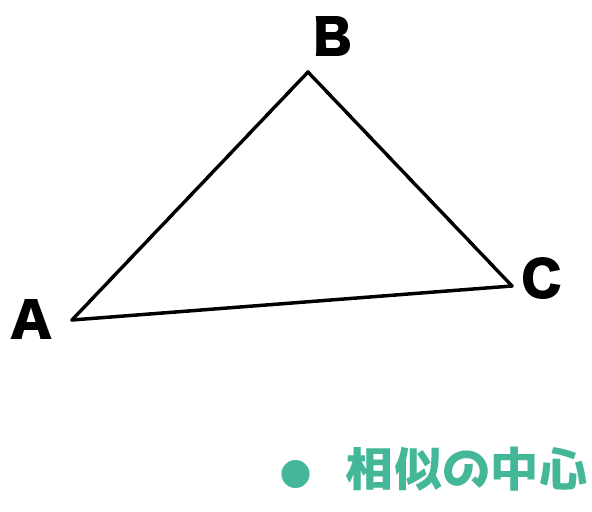
円周角 円と相似1 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 円と相似1 名前 右の図のように2つの弦AC,BDの 九点円の定理とは 九点円の定理とは,三角形と円に関する非常に美しい定理です.受験等に役立つことはほとんどないと思いますが,この定理の美しさを鑑賞する価値は十分あります.ぜひ,秩序だった様を存分に味わってください. 九点円の定理: $ abc$ について,以下の $9$ つの点相似の中心,相似の位置 相似な図形の対応する点どうしを結ぶ直線が1点で交わり、その点から対応する点までの距離の比がすべて等しいとき、その点を 相似の中心 とよぶ。



中学数学 図形の相似



方べきの定理と証明 相似と三平方の定理より Note Board
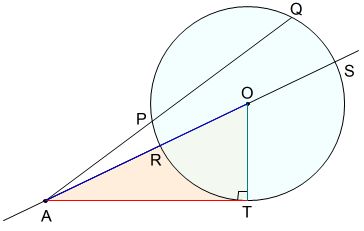
作図の方針は、相似の中心の利用です。下図が作図の全容です。 水色の小さい正方形と、赤い正方形 \(defg\) が相似 高校入試数学の難問円・相似と三平方の定理の総合例 相似な図形の例 直線, 正三角形, 直角二等辺三角形, 正方形, 正多角形, 円, 放物線, 直角双曲線, 正多面体, 球など これらはそれぞれ、一方を適当な率で拡大または縮小し、適当に平行移動、回転、鏡映を施すと他方に重なる。 このとき双方は形が同じであるが、大きさと向き(平面上では方べきの定理は、実生活では等式そのものよりも「円と直線の交点 \(a,b,c,d,p,x\) によって作られる2組の三角形がそれぞれ相似である」ということが重要な定理です。 「どの三角形とどの三角形が相似



中学数学 図形の相似



数学単元別シリーズの販売 教材出版 学林舎




17年11月29日 数学 円周角の定理 相似比を使った面積比と体積比 相似の証明 オンライン家庭教師 ウェブリー




1番は2 3なるのですが それは 相似の中心だからですか それとも Clear



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ




14 号 n アルキルボラジンの製造方法 Astamuse



三平方の定理の証明 相似を利用した証明3 Fukusukeの数学めも



平面の変換




これのやり方を教えてください 分かる方お願いしますm M Clear



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 3nen2 02 Pdf



中学数学 よく出る円と相似の融合問題 Pikuu




根軸 Wikipedia




中学数学 よく出る円と相似の融合問題 Pikuu



3つの相似の中心を通る線と円との極線 Geogebra



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
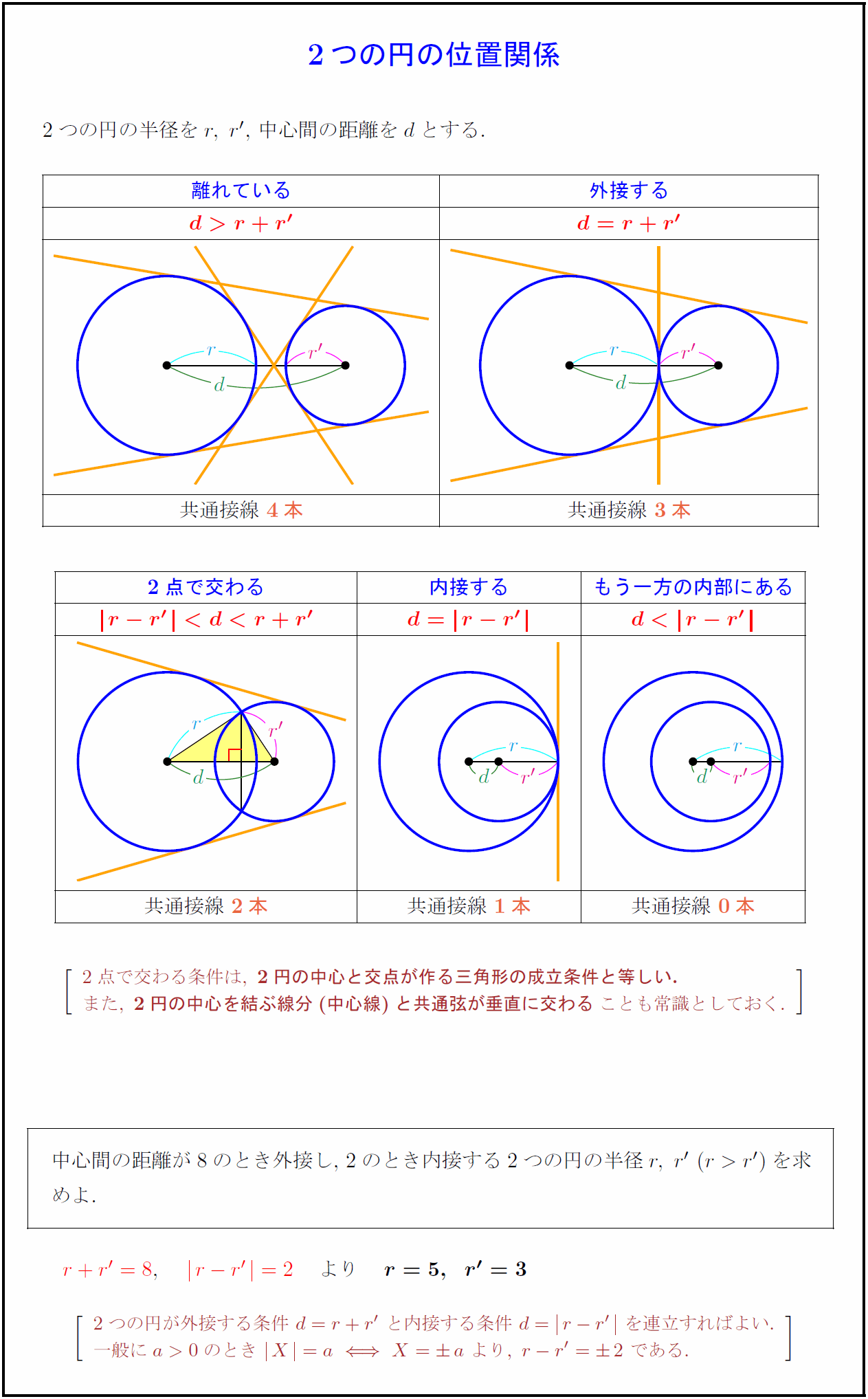



高校数学a 2つの円の位置関係5パターン 受験の月



Http Www Criced Tsukuba Ac Jp Renkei Msa Lessonplan Ooneda 2nd Medio Ooneda07 Jap Pdf




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear
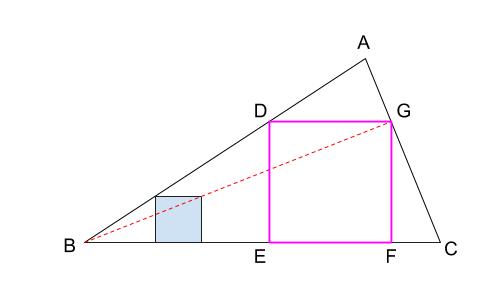



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su
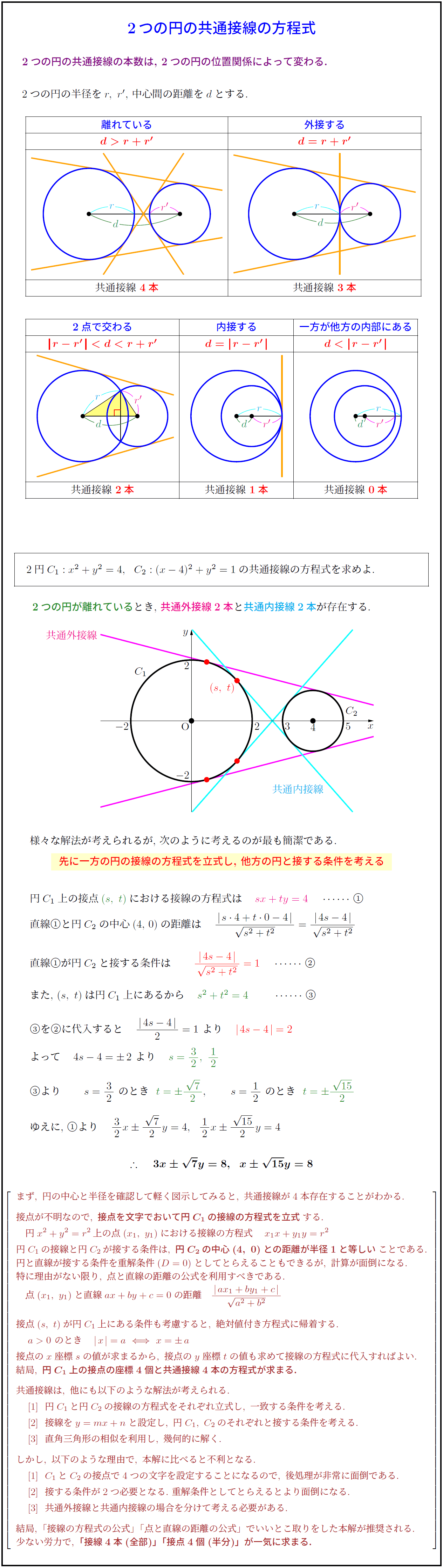



高校数学 2つの円の共通接線の方程式 受験の月



Mathematics 相似 6 円と相似 働きアリ The 2nd



Studydoctor相似の位置と中心 中3数学 Studydoctor
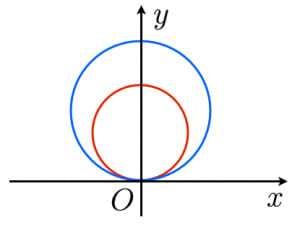



接する2つの円の相似の中心 高校数学の美しい物語
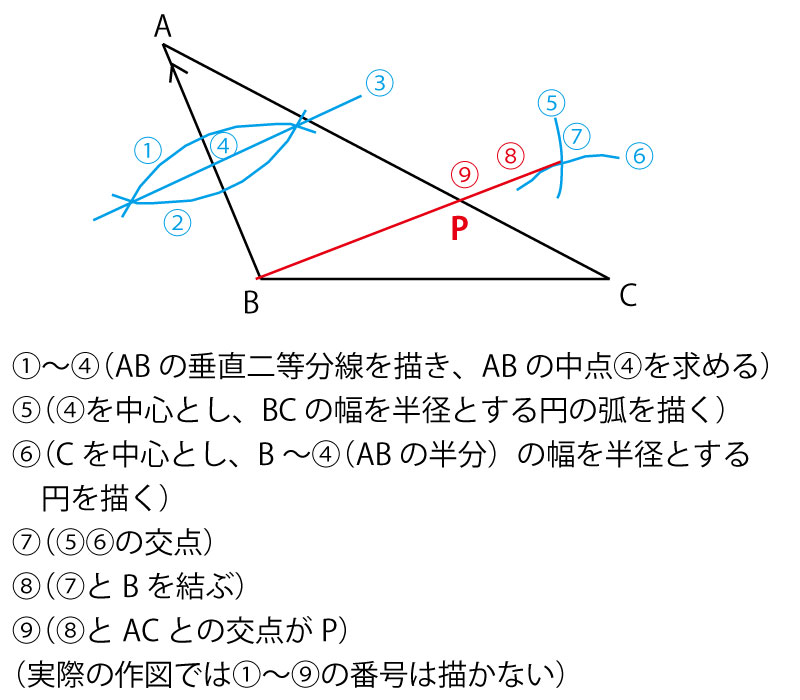



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Mathematics 相似 6 円と相似 働きアリ The 2nd



九点円
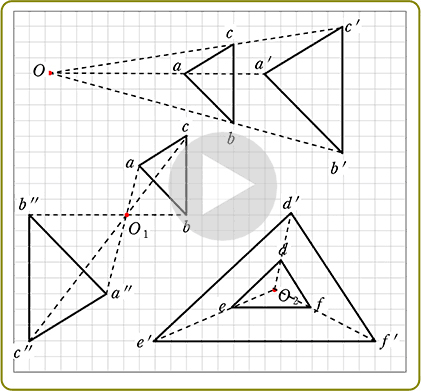



中学数学 図形の相似




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
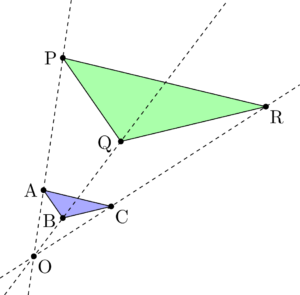



すべての放物線が相似であることの証明 大学入試数学の考え方と解法



相似の記号と対応 On Vimeo
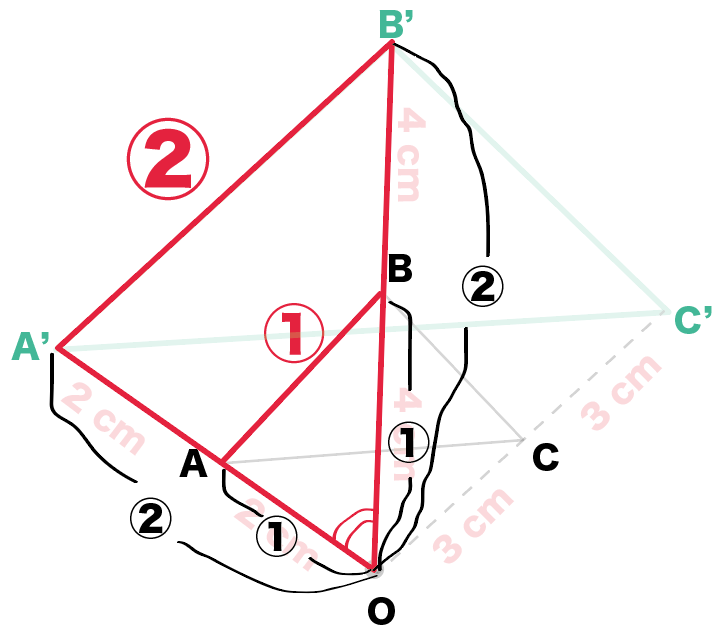



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



円と三角形 相似 中学から数学だいすき



放物線の相似性



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor



中学数学 図形の相似



円周角と比の問題 苦手な数学を簡単に




てなぐさみのメモ 相似の導入のあれこれ6 芳沢 新体系 中学数学の教科書 の場合



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
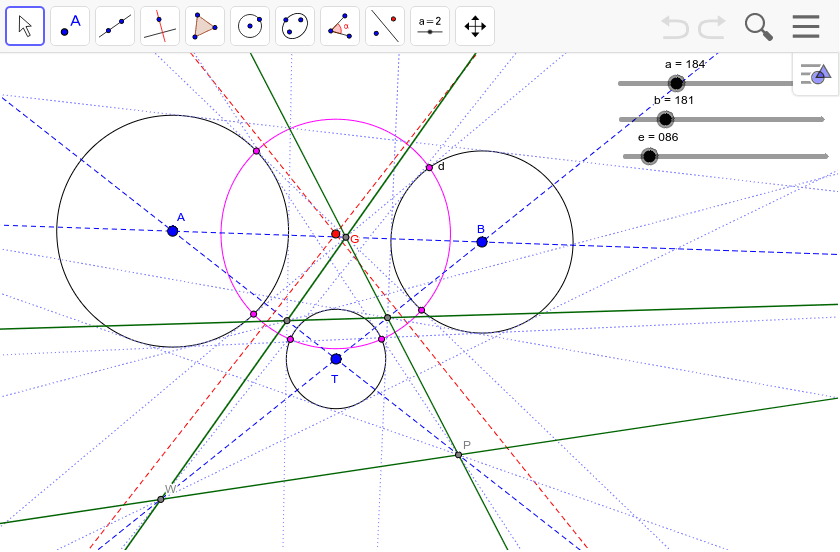



2つの円の相似の中心 Geogebra



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 3nen2 02 Pdf



すべての放物線が相似であることの証明 大学入試数学の考え方と解法



円周角の定理 理数系無料オンライン学習 Kori



Www Rimse Or Jp Research Past Pdf 8th Work06 Pdf



円と相似 チーム エン




共通外接線 共通内接線の描き方 ぬるいパースが描けるようになりたい




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月



円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者



相似の中心と作図 Youtube




アポロニウスの問題 Wikipedia



Mathematics 相似 6 円と相似 働きアリ




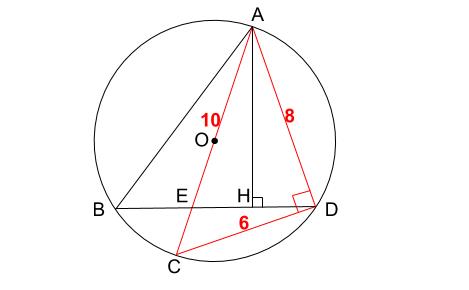
中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download



円 数学 Wikiwand



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files J3 Pdf




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



中学校数学 3年生 図形 相似な図形 Wikibooks




円と相似 無料で使える中学学習プリント




のんびりガチで物理学 数学編07 逆関数の微分 物理学 数学



放物線の相似性



円と三角形 相似 中学から数学だいすき




中3 相似の位置と相似の中心 Youtube



三角形のオイラー線 9点円及びその周辺の話題




接する2つの円の相似の中心 高校数学の美しい物語




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット



高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su



九点円



中学校数学 証明のコツ 入試問題 円
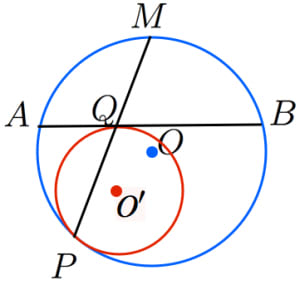



接する2つの円の相似の中心 高校数学の美しい物語



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ



放物線の共通接線のちょっとした小手技



平面における変換



アポロニウスの円 思考力を鍛える数学




円の相似拡大 縮小 Etc Den Of Hardworking



中3です 円の相似について質問です 全ての円は相似である というように Yahoo 知恵袋



Http Www Kumamoto Kmm Ed Jp Sugakubraindumps Pdf 3 5 Answer Pdf
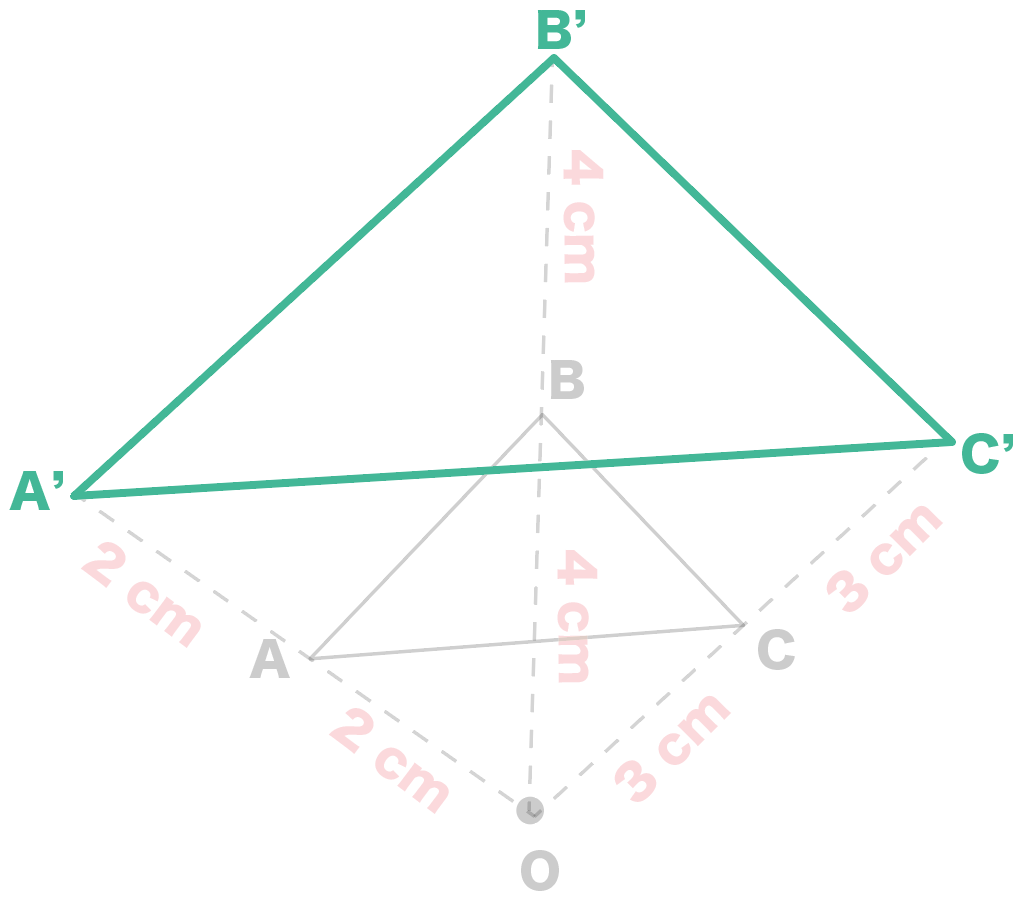



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
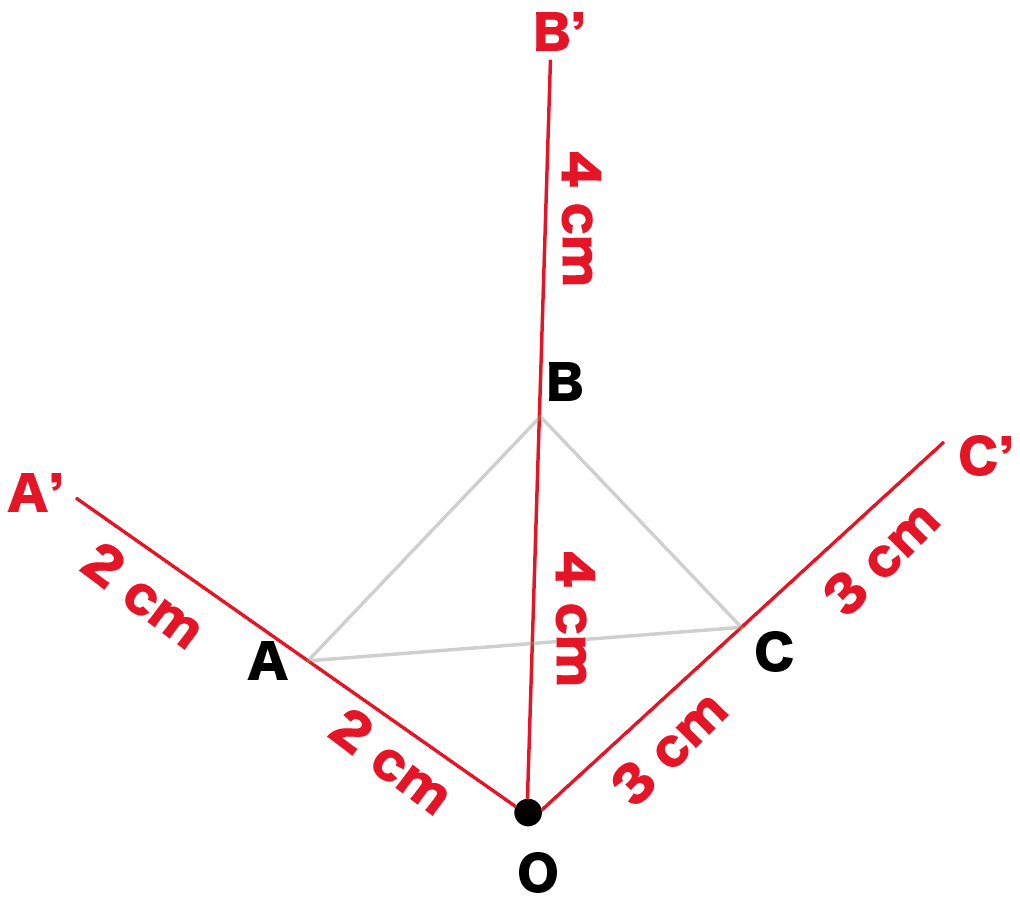



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋
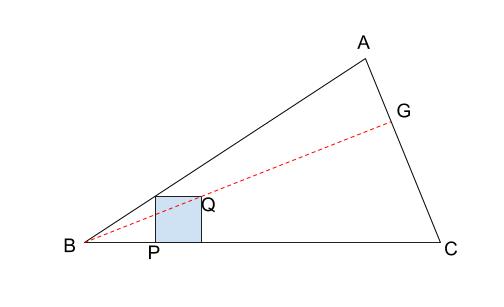



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



平面における変換
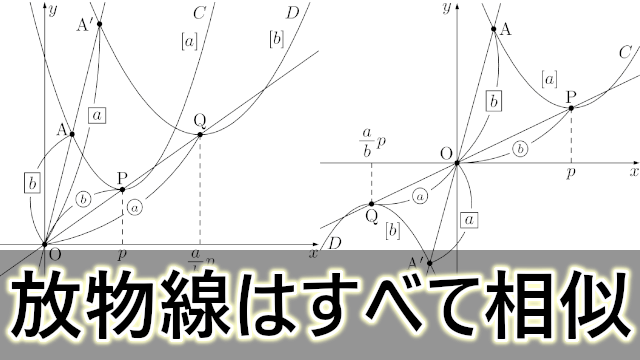



すべての放物線が相似であることの証明 大学入試数学の考え方と解法



0 件のコメント:
コメントを投稿