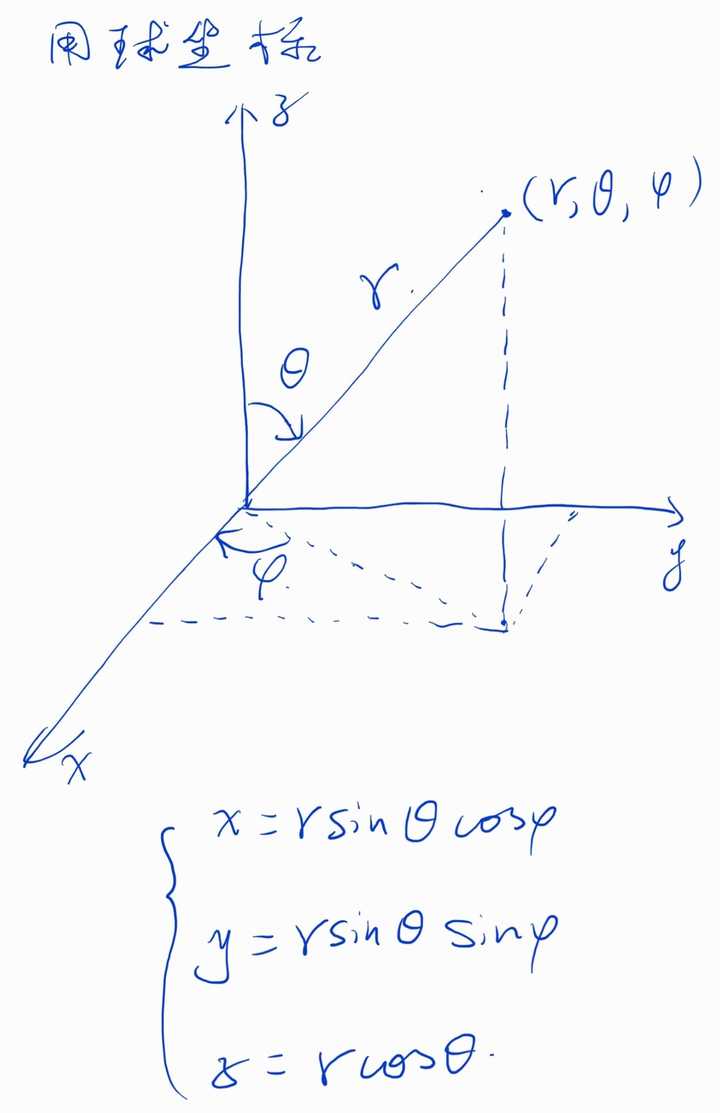
球欠,球台の体積と球冠,球帯の表面積 レベル ★ マニアック 積分 更新日時 球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。 結果を覚える必要はありませんが,導出方法はマスターしておきましょう。 目次 球を 球の表面積と体積を求める公式を紹介します。 シンプルに 球の表面積 球の体積 の2種類の公式だけです。とても重要なのでしっかり覚えておきましょう。「球の体積や表面積」 を求めよう。 ポイントは次の通りだよ。単純に、公式を覚えて当てはめていこう。 point 体積は(半径)を3回かける 半径は4cmだね。 公式にそのまま当てはめよう。 (1)の答え 表面積は(半径)を2回かける 体積の公式と混同しないように、注意して覚えよう。 (2)の答え
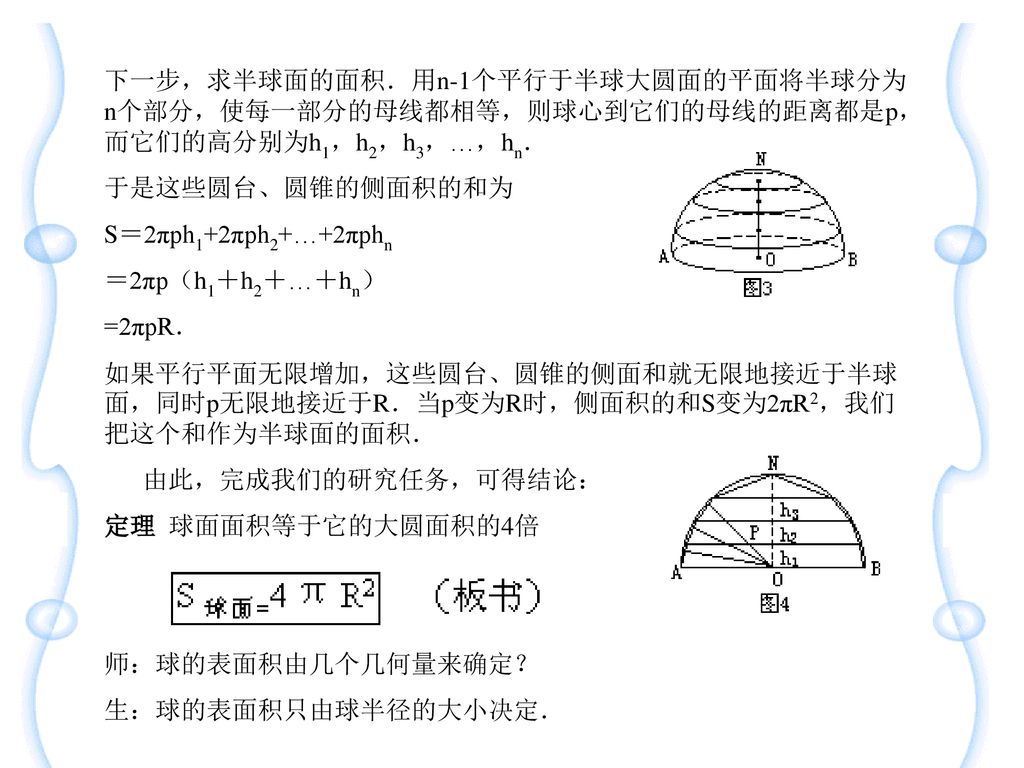
第二章 多面体与旋转体球的表面积教学目标1 使学生理解球的表面积公式的推导方法 并能熟记公式内容 Ppt Download
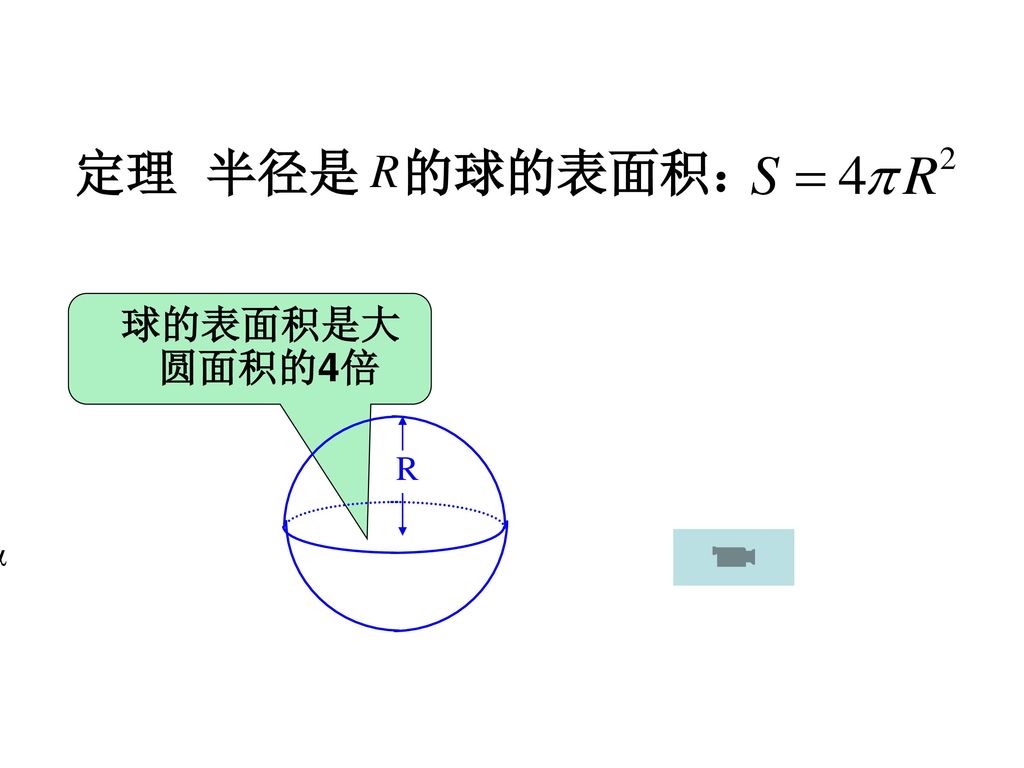
数学 表面積 公式 球
数学 表面積 公式 球- 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め球の表面積=円柱の側面積(アルキメデスの発見) 球の体積と表面積の関係から 球の表面積や体積を求める公式は,特に生徒が暗記に頼ってしまいがちな箇所ですが,暗記の覚え込みだけで得 た知識は,定着が悪く,応用も効きにくくなります。実験等を通してしっかりとイメージをつかませ



求圆的表面积公式 西瓜视频搜索
球の体積や表面積と、その球がちょうど入る円柱の体積や側面積との関係を、計算結果等で 確かめ、イメージとしてもっておきましょう。 2( 1 )球の表面積を求める公式: S=4πr2 ( 2)円柱の底面の円の半径: r ,円柱の高さ: 2r (Weblio 辞書 > 英和辞典・和英辞典 > 球の表面積の意味・解説 > 球 の表面積に関連した英語例文 例文検索の条件設定 「カテゴリ」「情報源」を複数指定しての検索が可能になりました。( プレミアム会員 限定) カテゴリ ビジネス (0) 法律 (0) 金融 (0) コンピュータ・IT (0) 日常 (0) ことわざ なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 ただし は幅 の部分の中央線である。 証明 より, (証明終わり) このような考え方を使って, 直円錐の側面積の一部分を考える。
今回は比表面積の意味、公式と計算、粒子径との関係、セメントの一覧について説明します。比表面積の単位は下記が参考になります。 比表面積の単位は?1分でわかる単位、読み方、公式、セメントの値の一覧 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもよって、球の体積Vは、円の面積をx 方向に積分すると、V=2∫0rπ(r2-x2) dxより、 V=2πr2x-(x3/3)0r=(4/3)πr3を導くことができる。 ②球の表面積の公式の求め方(1)球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう! ←今回の記事 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! 頑張っているのに思うように成績が上がらず、 「このままだと本番で数学60点が厳しいかも」 と不安に感じているあなた。 もしかして
球の体積・表面積~実験から公式を~ 球の体積・表面積 ~実験から公式を~ 兵庫県立星陵高等学校 中田 和彦 1.はじめに 数学・理科においては,今年度(平成24年度)から新学習指導要領の先行実施が始まった。この新教育課程では表題の単元『球の体積・表面積』は中学1年生へと移行され 球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。また、球の表面積は 等分される。このとき 等分された面積を とすると、 を底面とする正四角錐の1球の半径から体積と表面積を計算します。 半径 r 体積 V 表面積 S お客様の声 アンケート投稿 よくある質問 リンク方法 球の体積 110 /79件 表示件数 1 1306 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用目的 前立腺はくるみ大といわ




球表面积计算公式




球表面積計算球的體積 Jlxpis
裁ったとき切りとられた球の部分の表面積と切りとられた円柱の部分の側面積の 等しいことまで証明している。今読んでも感心するような厳密な証明である。し かし、これらの結果にどのようにして到達したかを「力学の定理による方法」と いう著作で説明している。そこで彼は、数学の問題余面積公式には、点から点へ pノルムがどのくらい変化するかを考慮した相関係数が含まれる。 p = 2 および p = ∞ に対してこの因子は 1 だが、 p = 1 ならば相関因子は √ n である(半径 R の ( n − 1) 次元 L 1 球面の表面積は √ n 掛ける L 1 球体の体積の R における微分係数)。球の体積と表面積 東京大学大学院数理科学研究科・教授 古田幹雄 1 円の面積と円周の長さ 半径rの円の面積はˇr2 です。 グラフv = ˇu2 のu = rにおける接線の傾きを求めてみま す。すると、答えは2ˇrとなります。これは半径rの円周の長さです。つまり、円の面積



椭圆球表面积公式球体表面积公式




求球体的表面积和体积 修也 Csdn博客
以下の語呂合わせで覚える方法が有名です: 球の表面積: 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に心配アール三乗」 ・側面積= 底面の周 × 高さ ・円の面積= 半径 × 半径 × 314(π) 半径 t の球の表面積を S (t) と書く。 三次元空間において、原点からの距離が t 以上 t \Delta t 以下の間にある部分(球殻)を考える。



球体表面积公式 怎样计算球体的表面积



Fsxuihbr P Sm
球の表面積の求め方の公式を1発でおぼえる方法 をひそかに伝授しよう。公式をおぼえたいときに参考にしてみてね^^ 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ n次元球の定義 n 次元球というのは n 次元の球です。 ちゃんと言うと、 n 次元空間内の「ある点」からの (ユークリッド)距離が「ある値」以下の空間を n 次元球と呼びます。 「ある点」を球の中心、「ある値」を球の半径と呼びます。 なお、今回は球の球の体積の公式と語呂合わせ 球の体積は 4 3 πr3 4 3 π r 3 となります。



Q Tbn And9gcqzkudsal3galmxwro65pdnhz6flxjjkxas5i6eaqlha2sgymk7 Usqp Cau



球体表面积公式 100查分网
球の表面積の公式の解説 半径rの球の表面積Sは S 4Sr2 円周の長さから円の面積を求める方法 を確認し、球の表面積と体積の関係と 比較する 例題12 球の表面積と円の面積の比較 結果が一致していることに関心を向け させる 展 開 15 練習40 球の表面積と円柱の側面積の比較 評価:表現球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる2つの平行な平板で囲まれた球台の表面積は、それぞれの球冠の表面積の差である。半径 で高さが と の球冠の場合、表面積は = , であり、地理座標である緯度 と を用いると = , となる。例えば、地球を半径6371 kmの球と仮定すると、北極(16年8月現在、北極圏である緯度6656°より北 )の表




球の表面積と体積の公式 数学fun




胶囊罐体 球冠高等于柱体半径 体积 表面积计算公式 三贝计算网 23bei Com
球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 \begin{equation} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation} となるので、確かに球冠の面積の公式で求めた結果と一致しています。 では、こちらも証明に入っていきます。球冠表面积公式推导过程 编辑 语音 假定球冠最大开口部分圆的半径为 r ,对应球半径 R 有关系:r = Rcosθ,则有球冠积分表达: 球冠面积 微分 元 dS = 2πr×Rdθ = 2πR 2 ×cosθ dθ 积分下限为θ,上限π/2 所以:S = 2πR×R (1 sinθ) 其中:R (1 sinθ)即为球冠的自身/ 数学公式集 / 体積・表面積;



1



球冠表面积计算公式 圣恩灵修网
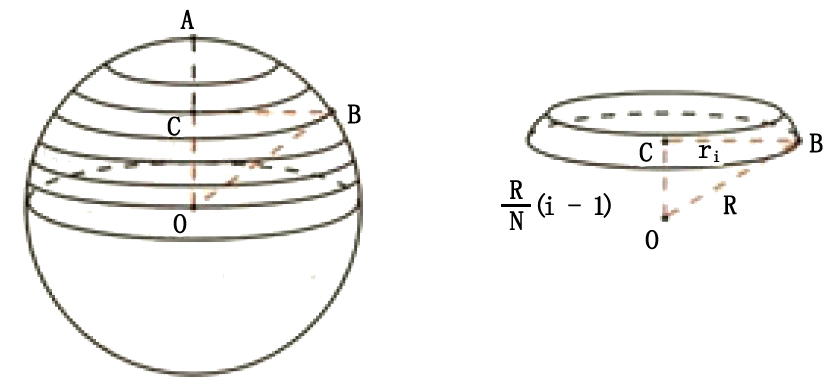
S:球の体積からスイカの様に三角錐を作って表面積を求めるしかないのかな。 t:球面三角法で球面の三角形の面積を求める公式を使えばできるかも。 s:でも、最初の三角形の面積の公式が求まるよ。 2 だから、α=2/π =底辺×r球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。 (2) 半径 2cm の球の体積と表面積は求めなさい。 (3) 半径 3cm の球の体積と表面積は求めなさい。 (4) 半径 4cm の球の体積と表面積は求めなさい。 (5) 半径 6cm の球の体積と表面積は求めなさい。 解答
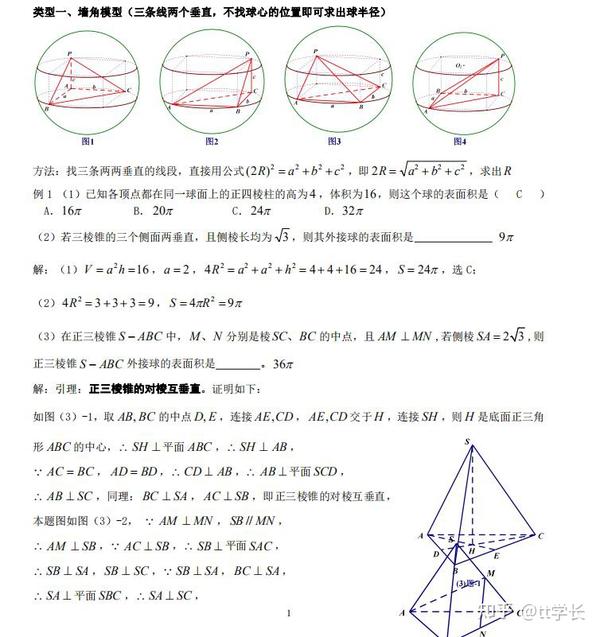



外接球体积切西瓜模型 八大外接球模型秒杀公式 外接球问题方法总结
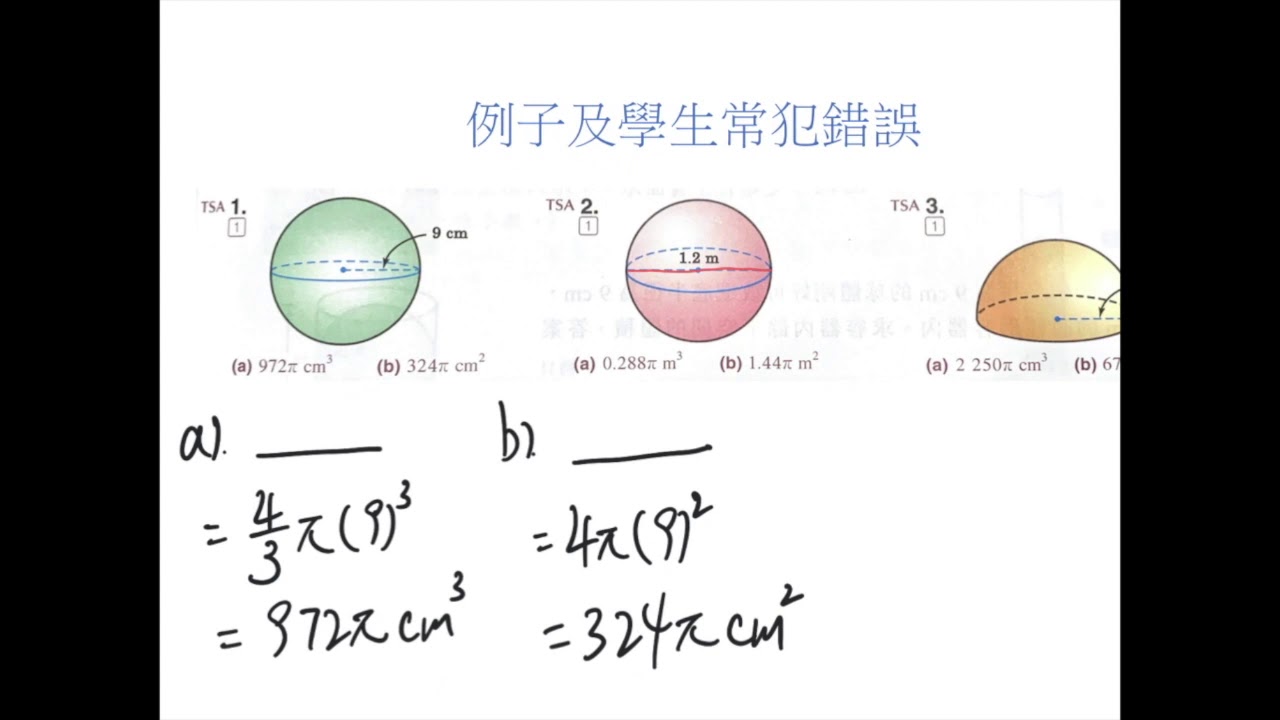



球體體積 總表面面積 Youtube
球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球体の表面積 S > 314πr2 (1)No004 半径 r の球の体積と表面積 球の体積 V m 3 は,球の半径を r m とすると以下の式で表されます。 球の表面積 S m 2 は,球の半径を r m とすると以下の式で表されます。 2 は,球の半径を r m とすると以下の式で表されます。




圆球表面积公式用微积分如何推导 知乎




旋轉體的側表面積040 正修科技大學微積分課程6 5 Youtube
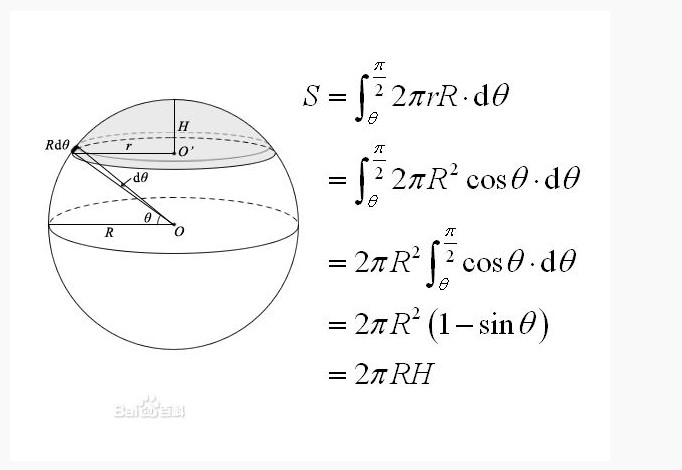



球冠表面積公式 計算方法 注意事項 中文百科全書



数学一分钟球的体积公式推导证明 哔哩哔哩 Bilibili




球體表面積公式sphere Java Mvc Liudong




球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客




初等幾何 球の表面積を求める 大人が学び直す数学



1




球的表面积和体积怎么算啊怎么计算球的表面积



写给5年级的学生 球公式是如何推导出来的 表面积



求圆的表面积公式 西瓜视频搜索




高考数学考点之空间几何体的表面积和体积 王羽课堂



球体表面积 球的体积和表面积 图文 叽叽歪歪吧



球表面积积公式推导 圆球表面积公式推导 公式学习




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



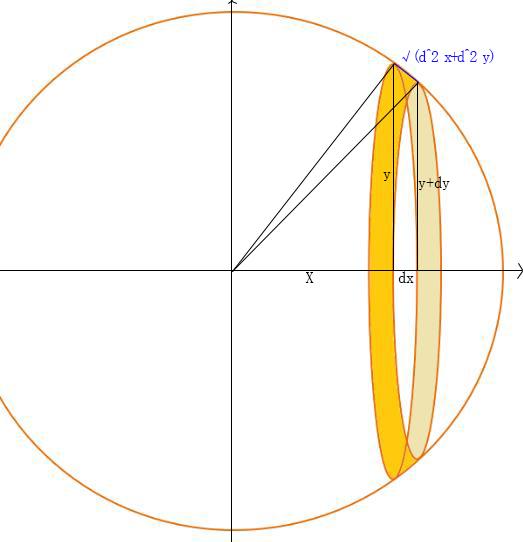
圆球表面积公式用微积分如何推导 球的表面积积分推导 德涵网




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社 自媒体学习平台




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




求半圆的体积公式和表面积公式 你搜我答




半球体积 表面积 截面积 球面积在线计算器 三贝计算网 23bei Com



球的体积公式和表面积公式 中国练字网




球的表面积和体积公式是什么



球的体积和表面积 西伯利亚 Ppt Download



球的表面积公式推导 万图壁纸网



圆球表面积公式推导球体的体积公式 表面积公式的推导




無料ダウンロード球表面積公式 ページを着色するだけ




球体的表面积和体积的计算公式 星火网校




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式




各類幾何體的體積與表面積的計算問題 每日頭條



球的体积和表面积公式怎么算球的表面积和体积 自媒体热点



Jfsu3vqa1 Gu9m




球的表面积公式是什么 球体积 表面积公式是




球体表面积推导过程 西瓜视频



圆球表面积 球体表面积的公式证明 篆体字转换器




圆球表面积公式用微积分如何推导 知乎




高考数学考点之空间几何体的表面积和体积 王羽课堂



球的表面积公式 球的表面积公式画法




體表面積表初中數學 幾何 面積與體積公式 Uhlwc




錐體體積公式



三棱锥体积公式 四棱台表面积公式 尚书坊



用积分推导球的表面积有哪些方法 球的表面积公式怎么来的 德涵网




椭球体表面积公式 椭球表面积怎么算 三人行教育网 Www 3rxing Org




第二章 多面体与旋转体球的表面积教学目标1 使学生理解球的表面积公式的推导方法 并能熟记公式内容 Ppt Download



Byh0jcsp0a4eqm




球表面積公式球體表面積 百度百科 Kmbymh




球體的體積球體 360百科翻譯此網頁 Gahzw



2



高中数学必修2教案 1 3 2 球的体积和表面积 淘文库




Wneqwztblxrfym




球體積的前世今生 每日頭條




表面積算法 ナノ粒子 粒度分布 比表面積 測定法 Itemn



球的表面積的求法 中學數學課 隨意窩xuite日誌




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt



求圆的表面积公式 西瓜视频搜索




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org




用感覺理解球體表面積公式 健康跟著走




球的表面积公式体积公式怎么写来求推导过程 计算机器在线计算



圆球体积公式 球的体积和表面积 趣闻趣事网



Q Tbn And9gctku R5xzpdmwkdjs1wzabajezbi10itywbdbzcvyi Usqp Cau




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科




球體表面積球體 表面積 體積 Vhjk




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科



球的表面积 球的表面积画法




非常有用的常用求面積 體積公式 非常有用收藏吧 每日頭條



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




球缺 一個球被平面截下的一部分叫做球缺 截面叫做球缺的底面 垂直于截面的直徑被截下的 華人百科



用微积分解答半径为a的球的表面积 作业 慧海网



图形公式大全表面积 万图壁纸网




表面积公式球




球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网




圆球表面积公式用微积分如何推导 知乎




球体积表面积公式




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com




球の体積と表面積 公式と計算問題と証明 Irohabook



如何不用微積分算個球 中科院物理所 微文庫



球体表面积公式球体表面积球体表面积 公式证明 爱华网




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站



圆球表面积公式的推导圆球体积公式的推导过程




球体体积 球体表面积公式 球体体积公式 简明教程



圆柱的表面积公式 圆柱的表面积公式画法




体积相同的球体和正方体 哪个表面积大球体积 表面积公式是




球的表面积 球的表面积画法




球體表面積及體積的推導 每日頭條



微积分计算球的表面积如何推算出球的表面积



0 件のコメント:
コメントを投稿