正多角形の作図をプログラミング 5年生の児童が,算数科の授業で,正多角形の性質から,辺の数や内角,外角の大きさなどに着目してプログラミングを行い,自分が描きたい正多角形を作図しました。 学校名 世羅町立甲山小学校 研究課題内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学 > 図形 > 内角の和から多角形を求める方法と一覧表 最終更新日 内角の和が x ∘ であるのは、 ( x 180 2) 角形 内角の和から、多角形の辺の数を求める方法を解説します。 正多角形 正多角形の概要 ナビゲーションに移動検索に移動正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。また、正偶数角形は点対称の図形でもある。辺の数が同じ正多角形どうしは全て互いに相似である。目次1 ユーク
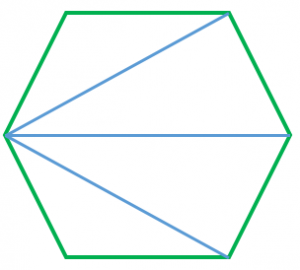
正多角形の内角と外角の大きさ 具体例で学ぶ数学
正多角形 内角 一覧
正多角形 内角 一覧- 多角形の性質:第5回 正多角形の1つの内角の大きさの2通りの求め方 多角形の性質 正多角形の1つの内角の大きさの求め方を2通りご紹介します。 ひとつは内角の和の公式を使う方法、もうひとつは外角の和を使う方法です。 記事を読む正多角形 † 分割対象の円弧が全円周の場合は,得られた点は正n角形の頂点となりますが, この場合,終り角は または と与えます。 と与えた場合,得られる点列は円周上正の向きに並び, とした場合は,負の向きに並びます。
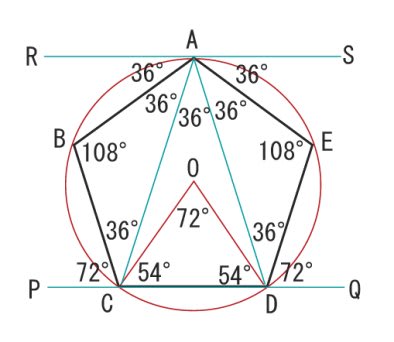



正五角形というだけで 分かる角度は 名寄 算数数学教室より
正多角形の一つの内角の大きさをもとにして正多角形をかくときのきまりに気付いている。 5 「円周」について知り,円周は直径の3倍以上4倍以下であることを理解する。 円に内接する正多角形の周の長さと直径の関係から円周の長さを近似して考えている。 正六角形の1つ分の内角は\(=1°\) 正八角形の1つ分の内角は\(=135°\) 正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法内角が150度ということは外角は180ー150で30度ということになります 外角の和は360度なので、360÷30で12となり、正12角形となります 内角の大きさが150度の時の正多角形の出し方を教えて欲
正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに相似で 多角形の内角の角度の合計を見つける 角度の合計を求めるには、 (n – 2) x 180という計算式を用います。 ここでの「n」とは多角形を構成する辺の数を意味しています。 また、最も一般的な多角形の角度の合計は下記の様になっています。 三角形(3辺から 正多角形の1つの内角の大きさの求め方を2通りご紹介します。 ひとつは内角の和の公式を使う方法、もうひとつは外角の和を使う方法です。 どちらの方法で解いても答えは変わらないのですが、正N角形のNの部分が大きくなると内角の和の公式を使う方法では途中の値が大きくなってしまい計算が面倒臭くなります。 その辺を踏まえて2つの方法を見ていきましょう
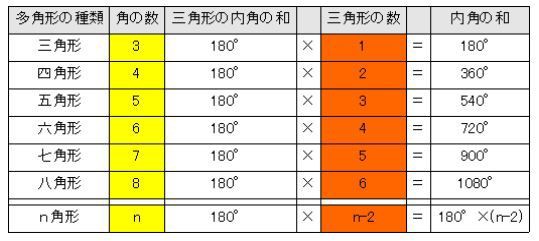
絞り開口が 正多角形 となる絞り装置を提供する。 例文帳に追加 To provide a diaphragm device whose diaphragm aperture is a regular polygon 特許庁 面が合同の 正多角形 であり、多面角がすべて一致している5種類の立体 例文帳に追加 any one of five solids whose faces are congruent 多角形の内角の和の公式 三角形の内角の和: 180° 180 ° 四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要もありません。 ではどのようにこの公式を導出するのか 4秒で計算できる!正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう!




正五角形というだけで 分かる角度は 名寄 算数数学教室より




正多角形の内角と外角の大きさ 具体例で学ぶ数学
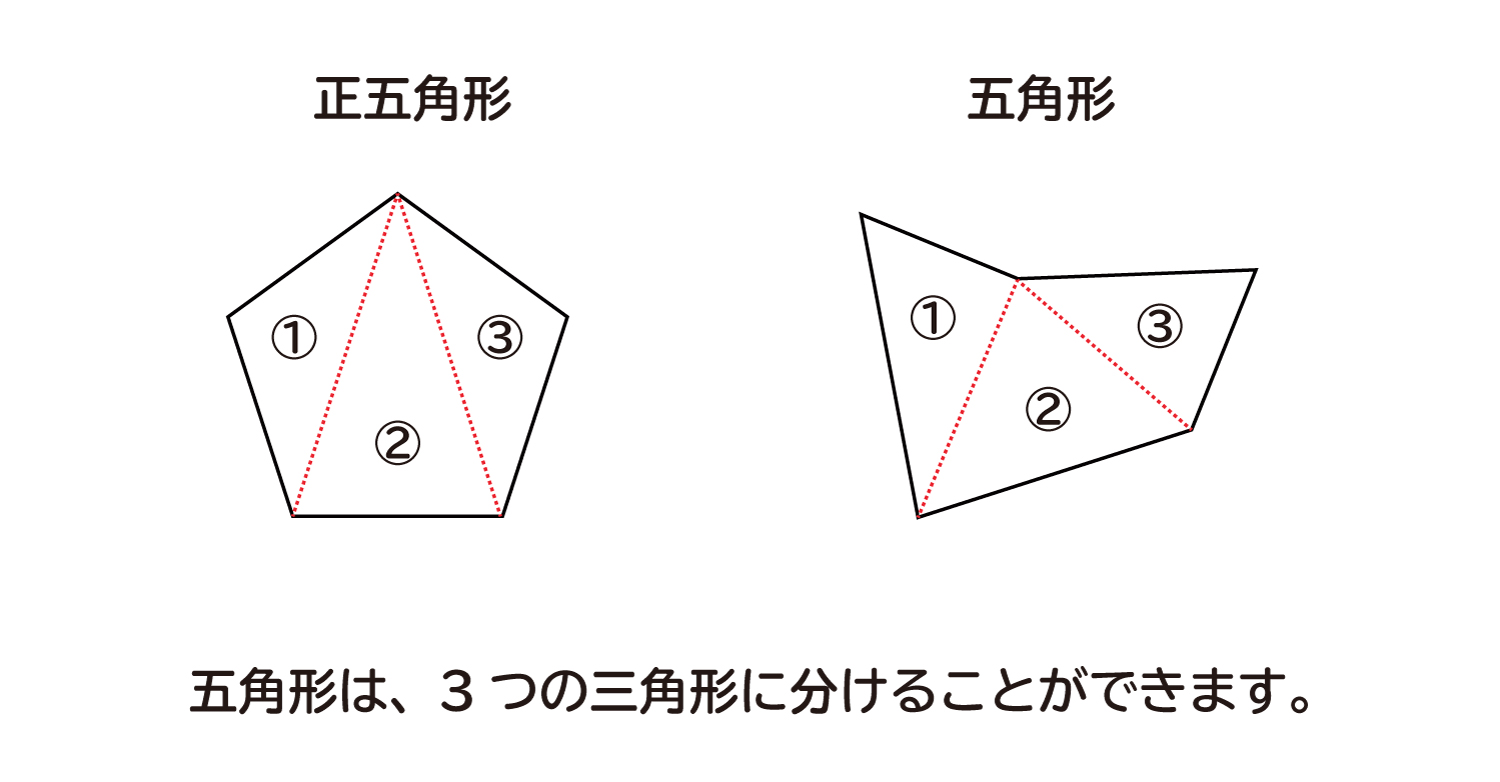
正多角形の1つの内角の大きさは,下記のように求めても良いです。 多角形の外角の和は360° なので,1つの外角の大きさは, 正六角形 正八角形 正十角形 が360°÷10=36°, 正十二角形 が360°÷12=30° と求まります。 よって,1つの内角の大きさは, 正六角形 が180正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに内角の大きさの公式の説明 正多角形の内角の大きさが、 180 ( n − 2) n という公式で計算できることを証明してみましょう。 n 角形は、三角形 n − 2 個に分割できます(例えば、六角形は四角形 4 個に分割できる)。 よって、 n 角形の内角の和は 180 × ( n − 2) 度になります。 正多角形の場合、内角の大きさは全て等しいので、一つの内角の大きさは、 180 ( n − 2




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
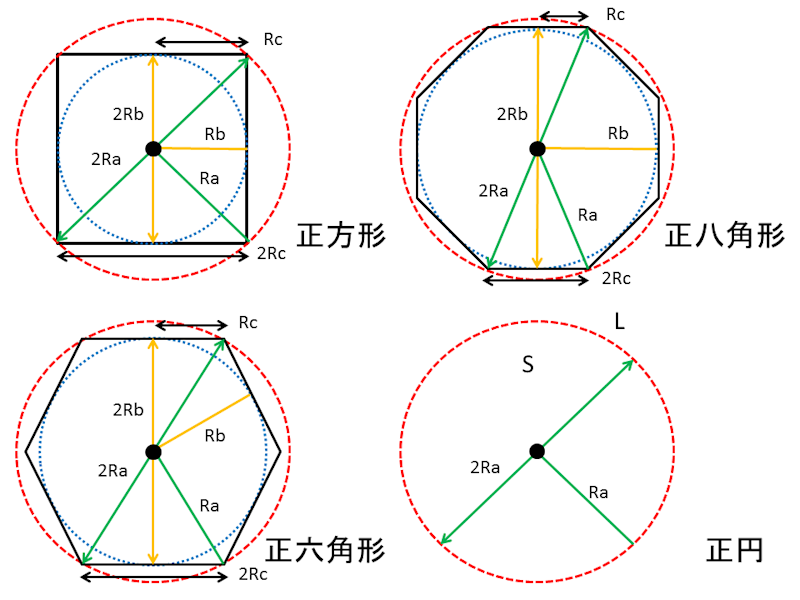
正十角形 (正十角形から転送) 正十角形十角形(じっかくけい、じっかっけい、英 decagon)は、多角形の一つで、10本の辺と頂点を持つ図形である。 内角の和は1440 、対角線の本数は35本である。 正十角形においては、中心角と外角は36 で、内角は144 とTap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history 正多角形の面積の公式一覧 1辺の長さがaの正多角形の面積の公式の一覧です。 調べるのに相当な時間がかかることが予想されますが(^^; 正三角形の面積の公式: 正四角形の面積の公式: 正五角形の面積の公式: 正六角形の面積の公式: 正八角形の面積の公式: 正十角形の面積の公
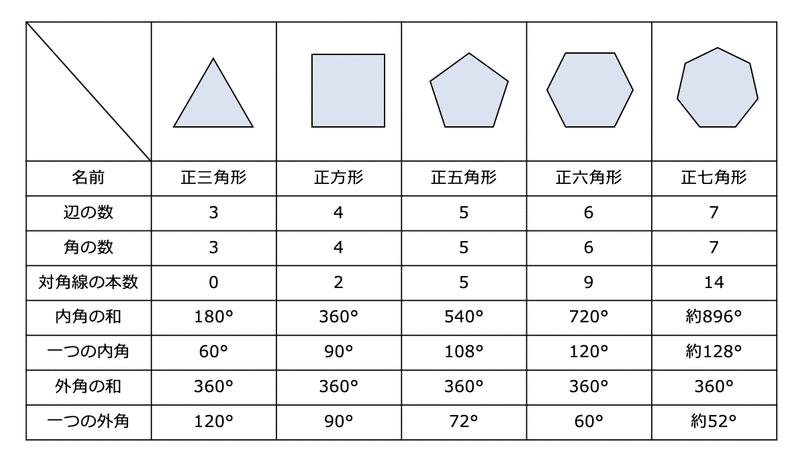



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報
すべての 辺 が等しく、すべての 内角 も等しい 多角形 を正多角形という。 正多角形は、 円周 を等分した点を順々に結んでできる多角形でもある。 この 円 の中心を正多角形の中心という。 この円は正多角形の外接円である。 また正多角形には、その中心を中心として内接円をかくこともできる。 辺の 個数 、したがって 頂点 の個数が n である正多角形を正n正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに相似で一つの内角が160度である正多角形は正何角形ですか。 Clear 数学 中学生 4年弱前 曜 (みかん🍊) 一つの内角が160度である正多角形は正何角形ですか。 で、何でnが、18になるのか教えてください! わかる人お願いします (´;ω;`)




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
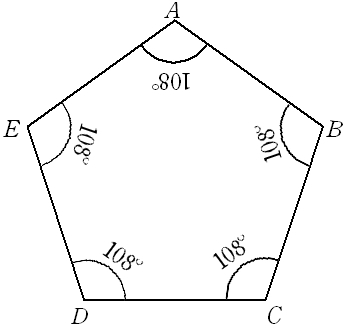
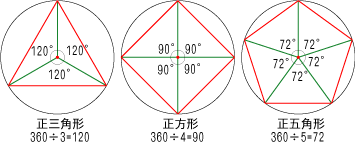
円と正多角形を考える (1)角aobの大きさは何度ですか。 上の図のように、円の中心から円周上のabcdeに直線を引くと、 等しい大きさの二等辺三角形が5つできます。つまり、角 が5つ。 すると、Afgに着目すると,三角形の内角の和は180°であるので, となります。 このような内角の大きさの関係は,角度を求める問題でしばしば利用されるので,公式として覚えておくようにしましょう。 例題 無料動画講義(理論) 1辺の長さがaの正八角形は、以下のように正方形を考えます 正方形の中に正八角形が入っている状態です 正方形の面積から4隅の青い三角形の面積を引けば、正八角形の面積が求められます 正八角形の内角は\( \frac{\times 4}{8} = 135^\circ\)です



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報




多角形の内角の和 は何度なのか を説明します おかわりドリル
多角形の内角の和の求め方については,小学校第5学年と中学校第2学年に学習することになっている。 その指導の基本的な考え方になっているのが,三角形に分割して内角の和を求めることである。 「中学校学習指導要領(平成29年度)解説 数学編」では数学・算数 図形 角度について 中2の数学でこういう問題がでました。 ある正多角形の1つの内角の大きさが、 その正多角形の1つの外角の大きさの5倍となる。 この正多角形の外角・内角と何正多角形を 質問No 多角形の内角の和/外角の和 である。 これはどのような多角形でも、対角線で適当に区切ることで (n2) 個の三角形に分割できることから導かれる。 正 n 角形の内角は全て等しいので、正 n 角形の内角は である。 n 角形の外角の総和は、 n の値によらず




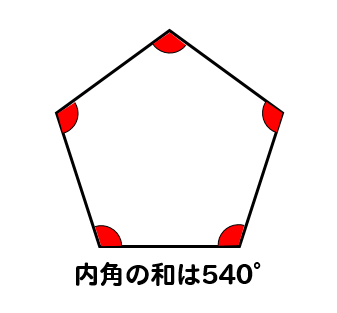
簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




内角の和 180 N 2 外角の和 360 教遊者
多角形の内角の和 一覧表と簡単公式による求め方 まず、多角形の内角の和を計算する簡単な公式がこれです。 n角形の内角の和 = 180 × (n – 2) この、 多角形の内角の和についてなるべくシンプル簡単に紹介していきます。 基本的な図形の内角の和は皆さん知っていると思います。 (三角形の内角の和) = 180° (四角形の内角の和) = 360° ここまでは大抵の人がしかし,正多角形で考えているので最大が1という約数になることが, 正多角形の1つの内角の和で最大のもの の文章から気づいているものと思われる。 次に紹介する生徒は,3種類しかないという根拠をしっかりと説明ができている(図5)。 正多角形は、Regular Polygonと言います。 A regular polygon is a polygon that is equiangular (all angles are equal in measure) and equilateral (all sides have the same length) (筆者訳)正多角形は、等角(角度がすべて同じ)で、 等辺(辺の長さがすべて同じ)の多角形である。 出




十五角形 Wikipedia




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
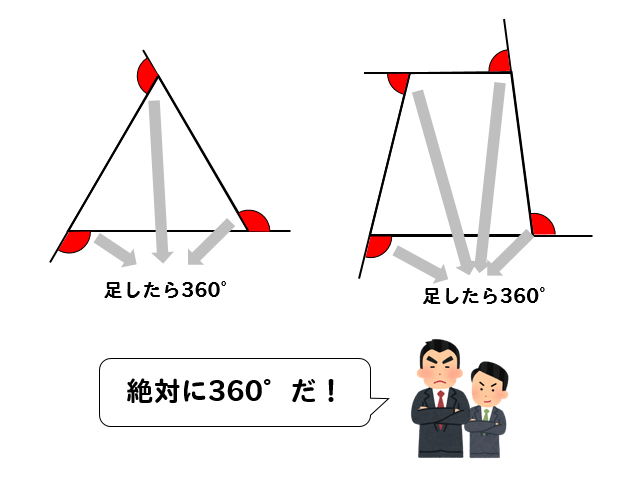
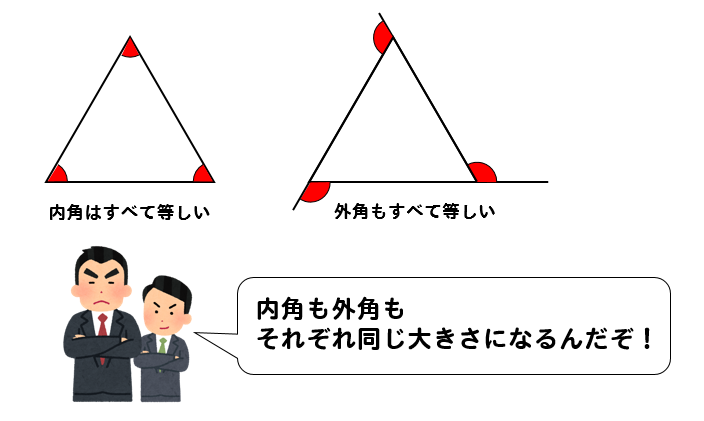
正多角形の1つの内角・外角を求める方法を問題解説! 正多角形の1つの内角・外角を求める方法を問題解説! If playback doesn't begin shortly外角は図2のような角では ない 各内角には2つの外角があるが,外角の大きさというときにはそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° に多角形の内角の和は「180°× (n-2)」で算定します。 nは多角形の辺の数です。 正8角形の辺の数は8なので「180°× (n-2)=180 (8-2)=1080°」です。 正8角形では8つの角度(内角)は全て等しいです。 よって、1つの角度は「1080÷8=135°」です。 今回は、正8角形(正八角形)の角度の求め方、内角の和と計算、外角、正9角形の角度について説明します。 多角形の内角の和




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト



茗渓予備校 科目別データベース
株式会社ベネッセコーポレーションのプログラミング教育の取り組みや、プログラミング教育に関する国内外のニュースや事例を紹介するWebページです。 小5算数 内角の大きさを求めて正多角形を作図しよう について紹介します。




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




五角形 Wikipedia




1つの内角の大きさが 1つの外角の大きさの8倍である正多角形を答えなさい この問題の Clear



多角形の内角の和 は何度なのか を説明します おかわりドリル
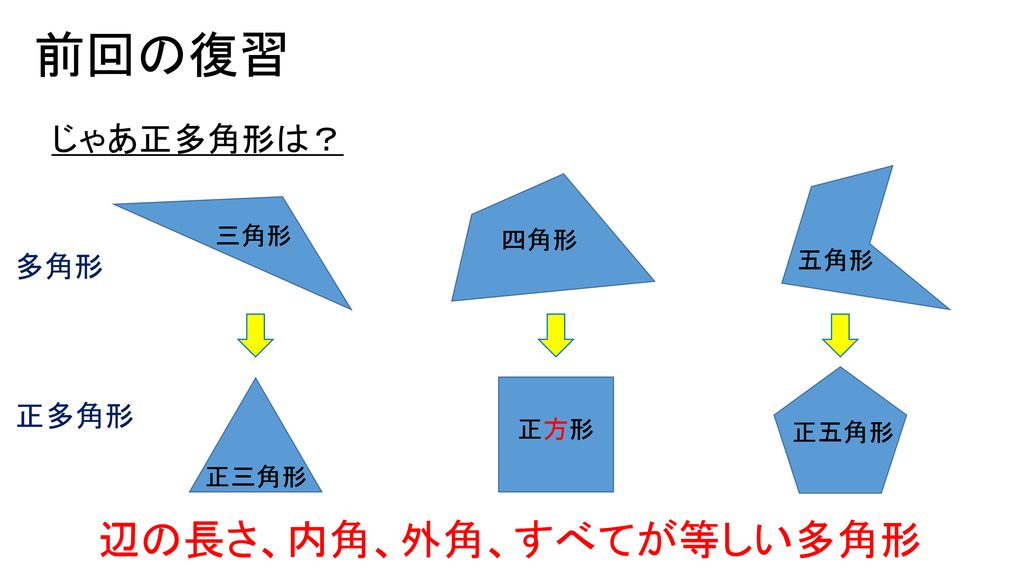



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download



1



正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




正多角形の内角と外角の大きさ 具体例で学ぶ数学
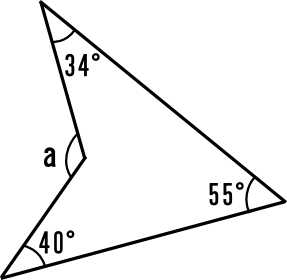



中学2年数学練習問題 図形の調べ方 多角形の内角と外角



南山中学女子部過去問題演習




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




内角の和 180 N 2 外角の和 360 教遊者
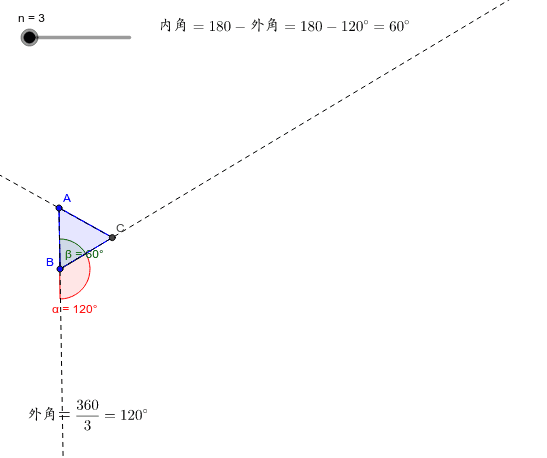



正多角形の外角と内角 Geogebra
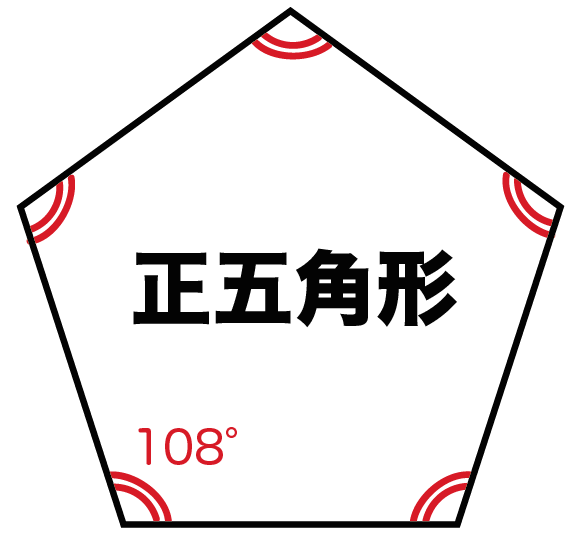



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



Www City Hadano Kanagawa Jp Www Contents Simple C050a Pdf
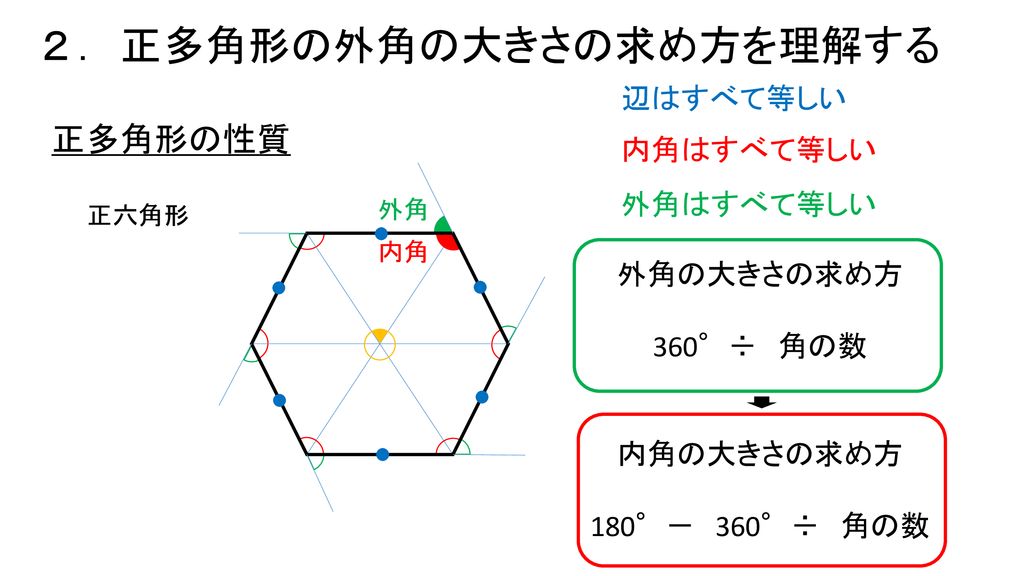



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




正多角形の1つの内角 外角を求める方法を問題解説 数スタ




小学5年生 正多角形 算数 Active Learning 学院



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




多角形の内角の和 外角の和の公式 数学fun
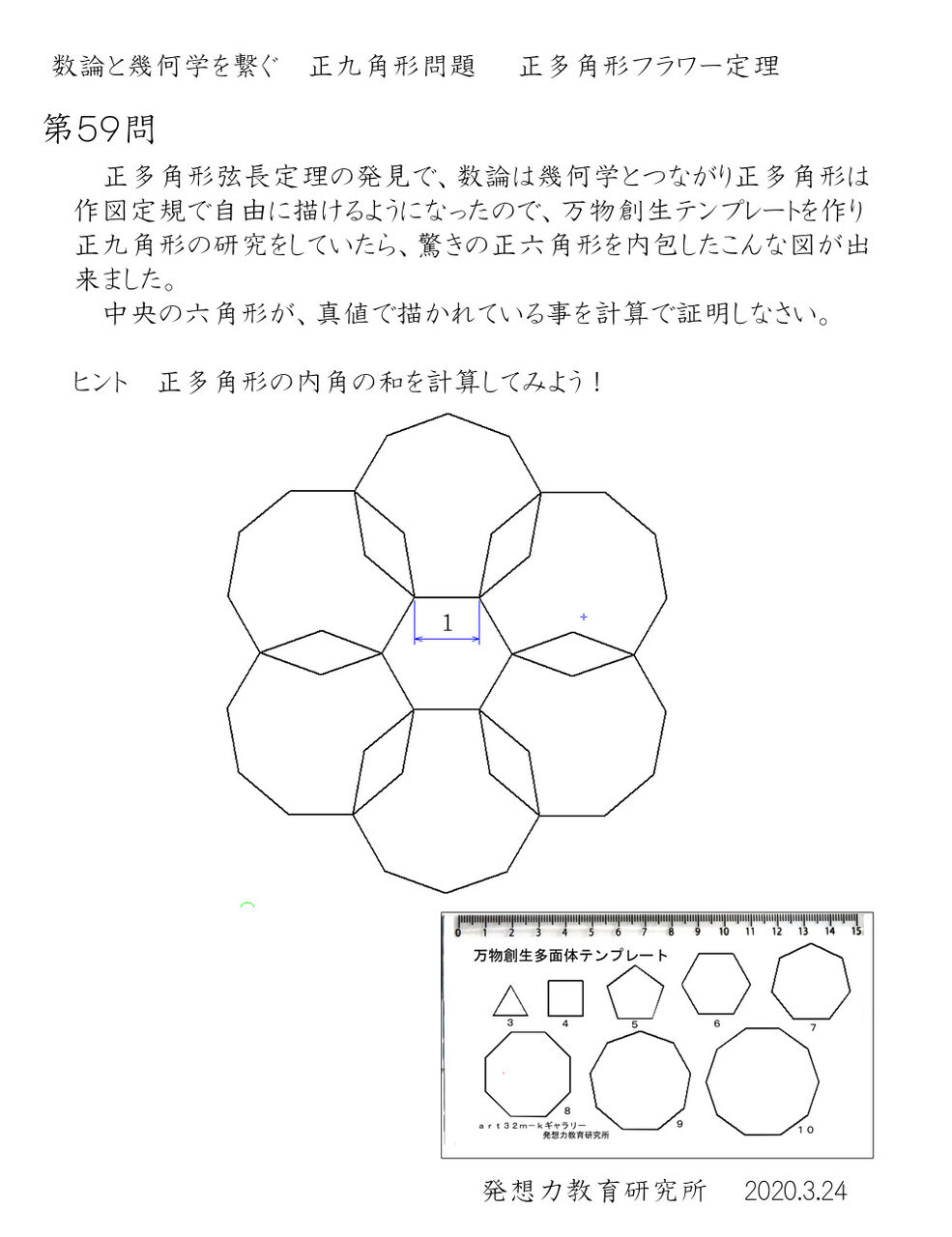



正9角形の証明問題 正多角形の間に存在する法則性を数論で証明する問題 発想力教育研究所 素数誕生のメカニズム




多角形の内角の和 は何度なのか を説明します おかわりドリル
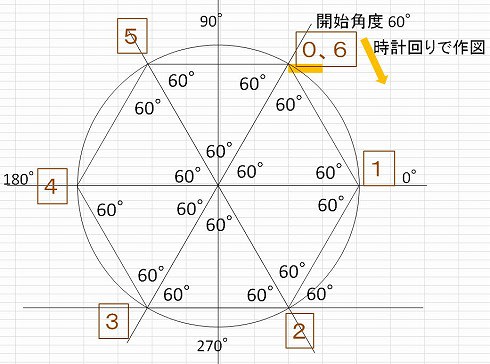



サッカーボールの型紙 エクセルvbaで正六角形を作図しますpart 2 日だまりのエクセルと蝉しぐれ




多角形の英語 五角形 六角形 八角形 12角形 正多角形など 英語独学マスター



1




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



1



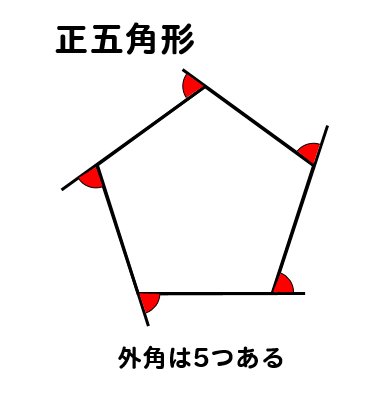
正五角形の内角 外角




一つの内角が160度である正多角形は正何角形ですか Clear



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



Descubre Como Resolverlo En Qanda



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




3 3 4 5 F Descubre Como Resolverlo En Qanda
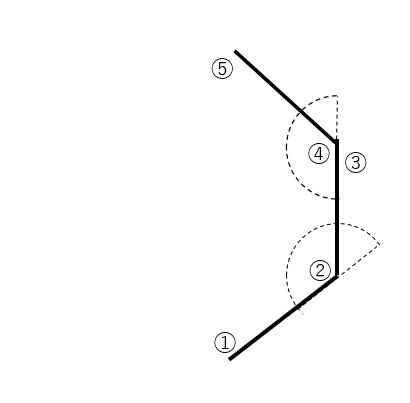



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



正多角形の作図 5年生 算数の広場




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




小学5年生 正多角形 算数 Active Learning 学院
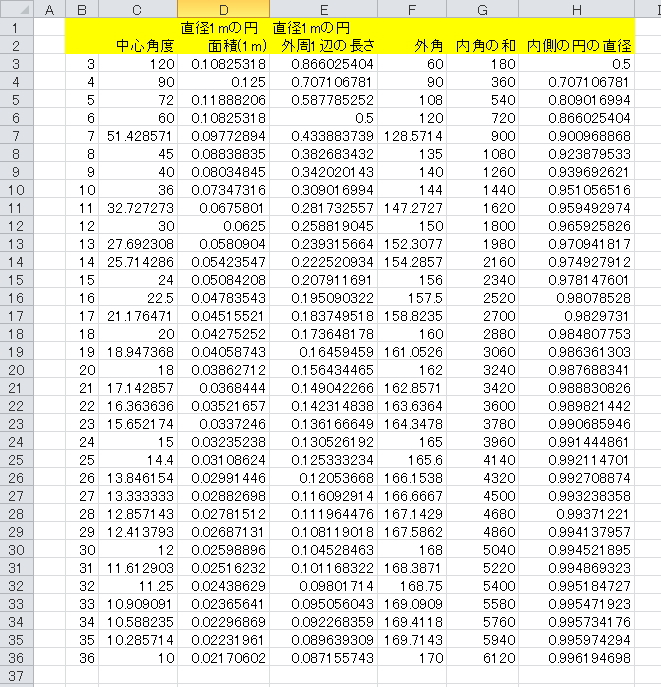



正 角形 正多角形 を表にしてみる エクセル関数の使い方



正多角形とは コトバンク




Sqrt3 1 1560 2 Descubre Como Resolverlo En Qanda
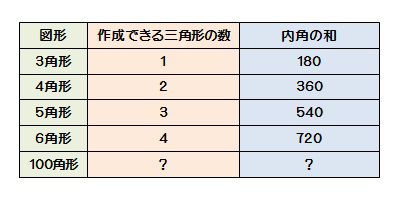



多角形の内角の和 算数の公式覚えてますか




多角形の内角の和の公式と外角の和を利用した角度の求め方




正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
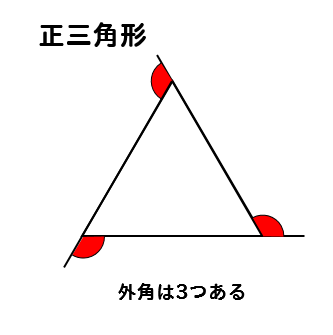



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



内角攻め それとも外角攻め すうがくラボのブログ




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




プログラムを考えて正多角形のきまりを見つけよう 未来の学びコンソーシアム



図形 正五角形の分解 父ちゃんが教えたるっ



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



正多角形の内角と中心角 家紋の描き方007b 夏貸文庫



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



正多角形 Color Cube ウィキ Atwiki アットウィキ
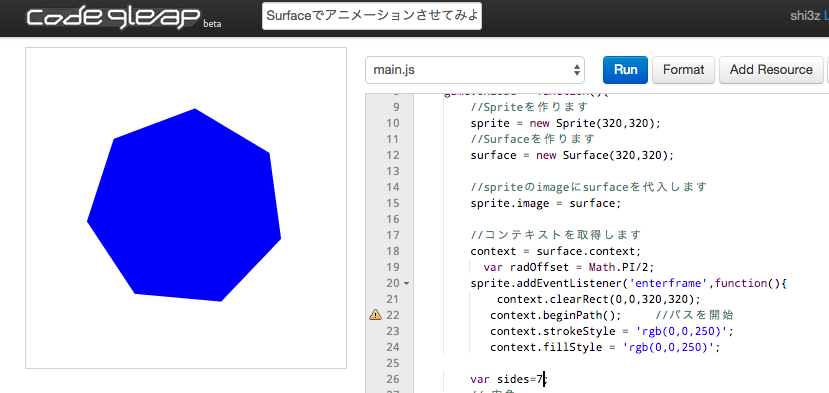



七角形の謎 または一周はなぜ360度なのか Wirelesswire News ワイヤレスワイヤーニュース



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




小5 算数 小5 54 正多角形 Youtube



内角の大きさが150度である正多角形 出石で数学をがんばりたい



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



正8角形 正八角形 の角度の求め方は 1分でわかる内角の和 計算 外角 正9角形の角度
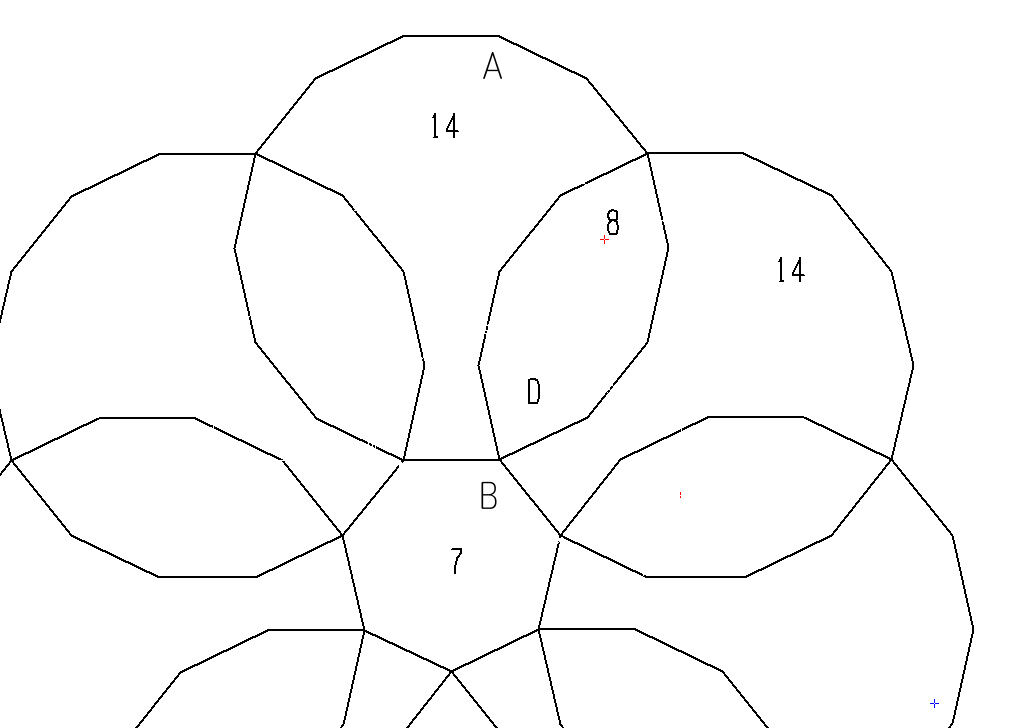



正多角形フラワー定理による 正七角形証明問題 解答編 発想力教育研究所 素数誕生のメカニズム



Happylilac Net Seitakakkei Ans Pdf




小学校5年 算数 正多角形の角の大きさ Youtube




一つの内角が160度である正多角形は正何角形ですか Clear
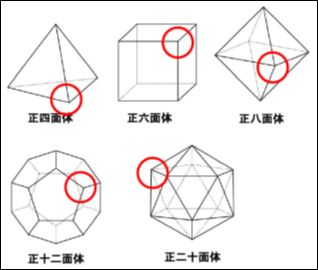



正多面体は5種類しかない 2 Only 5 Kinds Of Regular Polyhedron 2 同志社中学校




正多角形 内角が 108度 になるのは クイズ七種競技




1つの内角が162 となる正多角形を求める問題なんですけど やり方がわかりません Clear



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
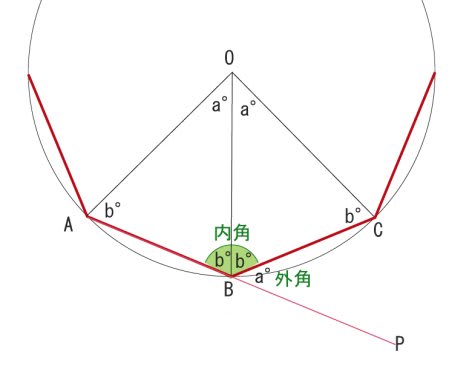



内角 と 外角 って 何だっけ 名寄 算数数学教室より



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




正多角形の1つの内角の2通りの求め方 算数パラダイス




1つの内角が150度の正多角形は何角形ですか 途中式も知りたいです Clear



南山中学女子部過去問題演習




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角
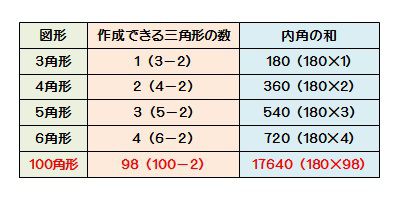



多角形の内角の和 算数の公式覚えてますか
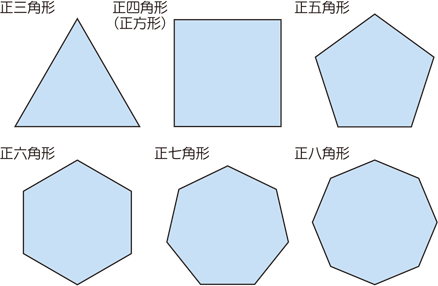



正多角形 算数用語集




内角の和 180 N 2 外角の和 360 教遊者



3
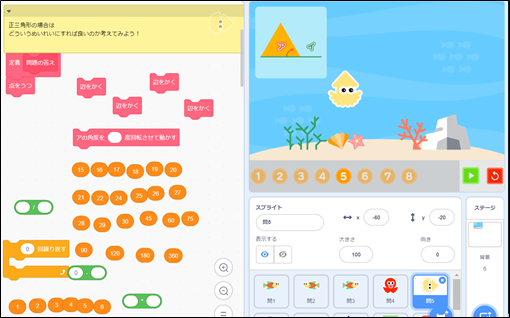



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報



0 件のコメント:
コメントを投稿