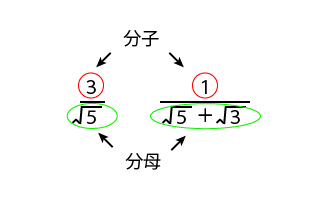
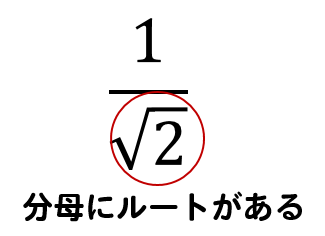
数学では、分数の分母にはルートを書かないというルールがあります。 計算の結果、分母にルートが入ってしまった場合には、分母を有理化して、ルートをはずしましょう。 この"有理化"が今回の学習のポイントです☆ ページトップへ戻る これ、知っ得!? 分数のルールについて確認し分数×分数=分数-分数? <先 生> より左辺の分母にある2数の差が1のときだと思います。 <先 生> そうだね。左辺の分母の2数の開きがキーになっている。①の場合は分母の2数の差をとると、 6-5=1 だね。この値1が分子の値と一致していることが大事なんだ。これを 1=6-5 と見てやる右辺は分数の形式ですので、数式ツール リボンのデザインタブで分数→分数(縦)を実行します。 分数(縦)が入力されました。 分母に入力したいのでカーソルキーを使って分母の四角を選択します。 「2a」と入力します。カーソルキーで分子の四角を選択

ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
分母が分数 ルート
分母が分数 ルート-下の計算はどうやってやるのか教えてくださ 掛け算や割り算の場合は簡単で、まとめてルートの中に数を入れて計算すれば良く、 × = = となります。 こんにちは! 普通は「分母を有理化(ルートをなくす)」して、分母にはルートがない形にします。 2/√ (5/3) = 2√3 /√5




S計算 部分分数分解編 おいしい数学
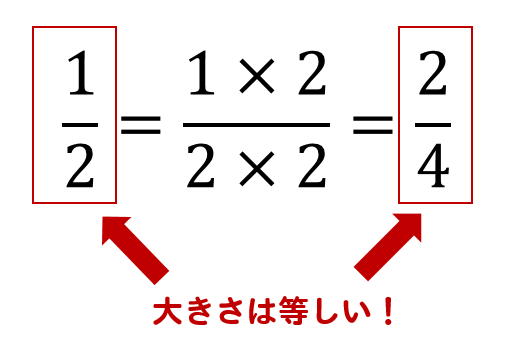
数学 分母にルートの分数がある場合の計算を教えてください! 下の計算はどうやってやるのか教えてくださ 数学 例えば16の4分の3乗は? 数学 4 数学の質問です。分数関数の分母に二乗がついていた場合はどのように計算したら良いのでしょうか? 二次分 数学 5 分数 とルートの計算 分数の計算です。 例えばですが、下のような計算があったとして約分した時に±が残りますよね。 その場合は分母につけたままでしょうか? そもそも分数の横に±がついた場合は分母と分子のどちらにかかっているのですか?? 初歩的な質問で申し訳あり分数というのは、分母と分子の両方に同じ数を掛けるのであれば 大きさは変わらないという特徴があったよね! だから、分母と分子の両方に同じルートを掛けることで 分数の大きさを変えることなく 見た目だけをチェンジすることができるってわけ! 有理化のやり方 分母にあるルートを
この不等式をどのように解きますか? 「両辺に (x − 1) (x − 2) (x1)(x2) (x − 1) (x − 2) をかけて分母を払おう」と考える人が多いのではないでしょうか? 実は,この分数不等式は 方法1.分母を払う方法 以外にも 方法2.通分する方法(おすすめ) や分数や小数の場合はどうやる?←今回の記事 平方根、ルートの値を語呂合わせ!覚え方まとめ a√bの形に変形するやり方とは? 平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ!分母に分数を含む式 ここでは、分母に分数を含む式の計算のしかたについてみていきましょう。 次の式を簡単にしなさい 難しい分数式を考える前に、簡単な分数を例に考えてみましょう。 この分数式について考えてみます。
分数(有理数)の指数が付いている式は累乗根で表される式と同じものです.多くの場合,分数の指数を使って計算する方が累乗根のまま計算するよりも簡単になります. 分数(有理数)の指数の定義 a>0 であって m, n が正の整数であるとき a mnn = n√(a) 一般に,分数関数は(分子)÷(分母)の割り算によって商と余りに分けると,「分子の次数<分母の次数の形」 (数研の参考書で「分数式は富士の山」と呼ばれるもの) に変形することができる.この変形により,分数関数の不定積分を求めるときは,分子の次数が分母の次数よりも低いルートの付く数があるといっても分数やルートの計算ルールは変わりません。分数の計算は下記が参考になります。 分数とは?1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方 ただし分母にルートの付く数がある場合、有理化(ゆうりか)を行い、より簡単な形で表します




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
ですから普通、分数全体にマイナスの表示をすると思います。 ルートが分母に来る表示って沢山ありますよ。例を挙げると、虚数である i の平方分母の有理化1 分数の分母に平方根がある場合に分母の平方根をなくすことを 有理化 という。 解説動画 ≫ 分母を有理化せよ。 5 3 7 8 9 5 12 ① 5× 3 3 × 3 = 5 3 3 a × a =aという性質を利用して、 分母にある√と同じ√を 分母、分子にかける。算数数学個別指導の中山先習塾の映像授業です。 高1「実数、無理数、根号、ルート、計算規則、分母の有理化」 中山先習塾の公式サイト( https




小数や分数のルートの外し方 分数の の外し方は知っておくべきだ 中学や高校の数学の計算問題




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題
分子も分母も関数の分数関数 さて、それではこのような分数関数の微分はどのようにして求めるのでしょうか?次から見ていきましょう。 2 分数の微分のやり方 結論から言うと、分数の微分はどちらも公式を使って求めることができます。それぞれ見てとなります。 x x を微分せよ。 を利用します。 分数関数の微分公式 f ′ ( x) g ( x) − f ( x) g ′ ( x) g ( x) 2 より、 例題3: 1 x 3 1 を微分せよ。 分子が 1 のバージョン(計算が簡単)です。 商の微分公式より、 分母は展開しなくてもOKです(もちろん展開 ルートの計算で分数の分母を有理化しないといけない理由とは? 中学校の数学で、分母にルートがついた数があることを嫌います。 と、言うよりもやっちゃダメという感じですよね。 高校生になると一部分母にあってもいい感じにはなりますが、中学校



有理化 もう一度やり直しの算数 数学




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ
ツイート 無料ダウンロード・印刷できる小学5年生の算数プリント。 分母のちがう分数を、通分、約分して引き算する練習問題です。 異分母の分数の引き算(1) 答え 異分母の分数の引き算(2) 答え 異分母の分数の引き算(3) 答え4 分数が入るルートの計算方法 5 数学 分母にルートの分数がある場合の計算を教えてください! ルート10の連分数表記 本稿では、 √10 10 の連分数表記について見ていきます。 まず、次の式をご覧ください。 中学のとき、分母に 無理数 が来たときは有利化しなさいと習いましたが、ここではその逆を行っています。 3 √10 = 6 1 3√10 (2) (2) 3 10 = 6




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




分数を有理化しよう 分母にルートが2つある時はどうしたらいいの さびねこ中学校
分数の足し算 分数の足し算は ①:2つの分数の「分母」が同じになるようにそろえて(通分して)から ②:2つの分数の「分子」を足し算をして ③:最後に「約分」をする。 この 3つのステップをふむのがコツ です。 ここでは、「2/3 1/12」を計算してみましょう。ルートの付いた分数の引き算、分母の関係 ルートの付いた分数の引き算も、前述したようなルートの計算の規則が適用されます。加えて分数の計算の規則も重要です。分数の計算については下記が参考になります。 分数とは?1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方分母と分子を上下に分けて分数が表示されます。 入力した分数を編集する方法 挿入された分数を編集する場合は、フィールド コードを表示してから編集します。 フィールド コードを表示します。 Alt キーを押しながら、F9 キーを押します。 分子と分母の数値を編集します。 変更したい任意




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題
①ルートの中身を簡単にする 分数を書くときは \(\dfrac{6}{4}=\dfrac{3}{2}\) のように可能な限り「約分」をしますよね。 それと同じで、平方根を使って数を表すときは ルートの中身を可能な限り小さな自然数 にします。 分母の「9」と分子の「12」の共通の約数に3がある。 ってことは、3で約分できるはずだから、 9分の12√3 = 3分の4√3 になるね。 これでルートの分数の計算は終了だ! まとめ:ルートの分数の計算は総合格闘技だ! 平方根の分数の足し算・引き算はどうだっ分数のわり算を扱うときには「包含除」で考えることが理解するうえでの近道となります。分数のわり算は、以下のように計算しますね。 4 ÷ 2 5




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学
分子(分数式の上の部分)入力枠に移動し、x を入力後、 を利用し2乗部分を入力する。 下の矢印で、添え字入力を抜け、キーボード入力により 1 を入力する。 下の矢印を何回か押し、分母入力枠に移動する。 を利用して、ルート機能を選択する分母分子に 3 をかけることによって、分母のルートが外せます: 1 3 = 1 × 3 3 × 3 = 3 3 このように、分母が n という形の分数については、 分母分子にそれぞれ n をかける ことによって分母を有理化することができます。 分数の分母にルートがある?? そんなときは、分母を有理化してやろう。 平方根を簡単にして、 分母のルートを分子と分母にかければいいのさ。 ゆっくり有理化になれていこう。 そんじゃねー Ken Ken Qikeruの編集・執筆をしています。 「教科書、もうちょっとおもしろくならないか



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係




根号をふくむ足し算と引き算 の分数をふくむ場合 Youtube
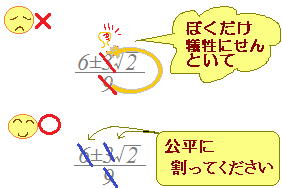
※ 分母は「なるべく」正の数になるようにします.(高校以上では様々な場面で,分母を負の数のまま使うこともありますが,中学校の基本の段階では,「分母は正の数にする」ように決める方がよい.) ※ 上の式で,分母と分子を −2 で割ると,それぞれ符号が変わりますので




4 のlog36の 乗てどうしてルート6になるんですか Clear




高卒認定試験数学の平方根 分母の有理化の解き方を解説 坂田先生のブログ



Math 超簡単 有理化 分母に根号がない形にする 働きアリ




分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題
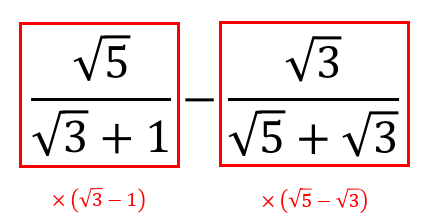



ルートの分数計算 問題解説で完全マスターだ 数スタ




分数の割り算の計算方法 どうして分子と分母を入れ替えて掛け算する




中学数学 平方根 のコツ 有理化 加減乗除 展開




部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ



根号計算 約分




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo



Q Tbn And9gcqrowgvqn H0mpsul5gslm5oso Kohgdb3kvug Q8m84kyw0il Usqp Cau




平方根 ルート の計算をおぼえよう しろカスと学ぶ中学数学 理科
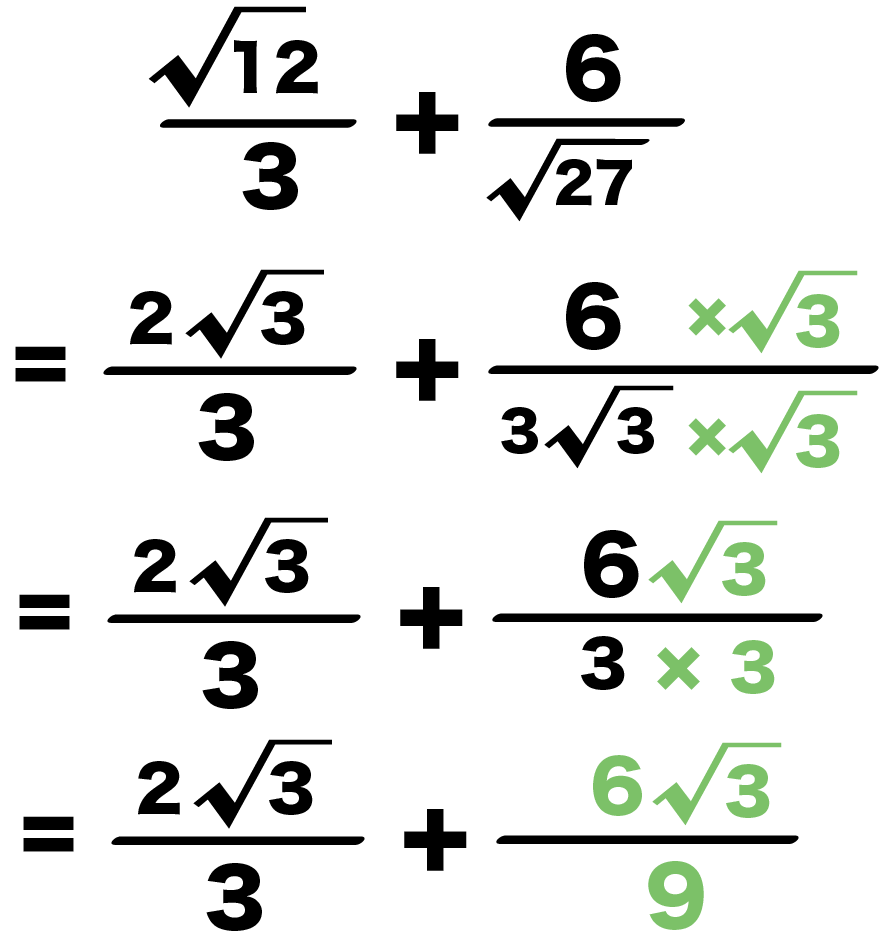



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




これで完璧 平方根の基礎 中3数学 中学生の勉強法




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題
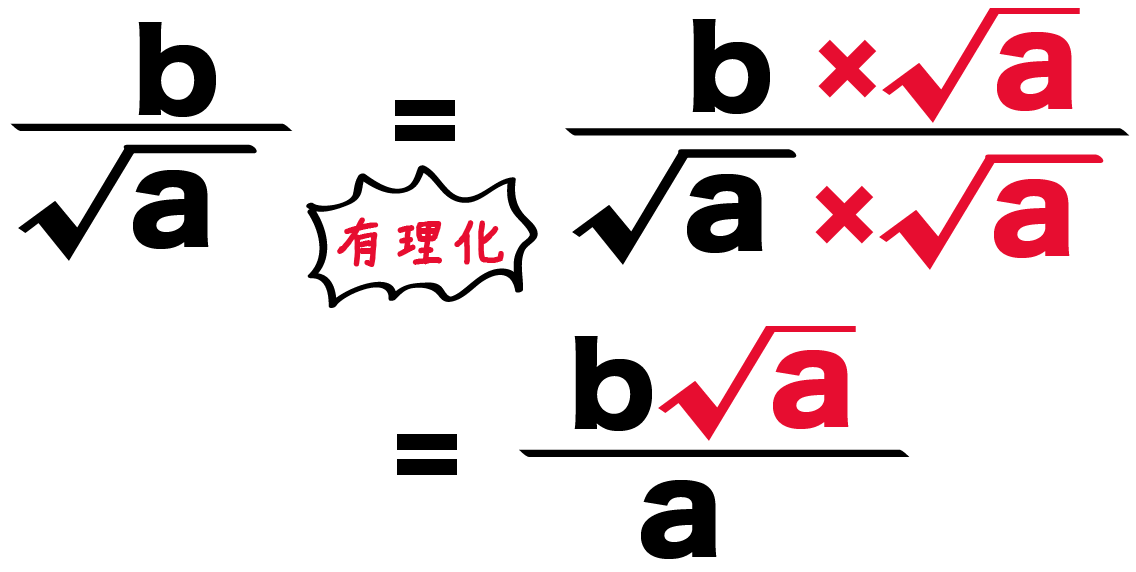



平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
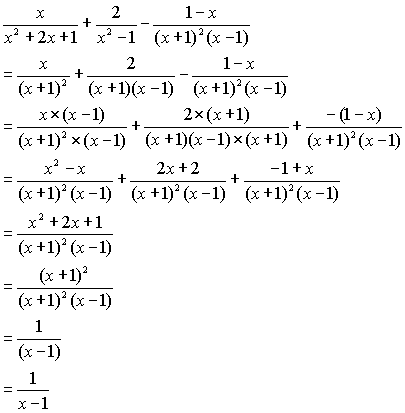



分数の復習と分数式の計算
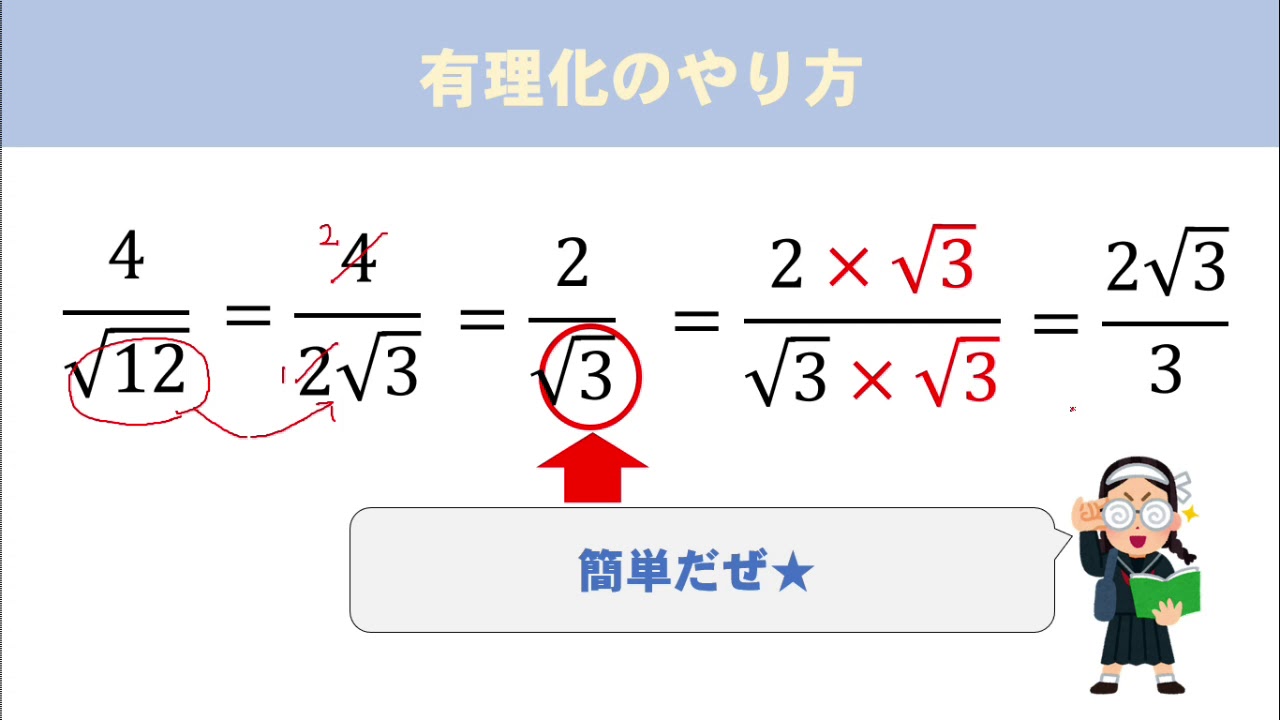



平方根 分母の有理化のやり方はこれでバッチリ 数スタ



3




高校数学 数列の極限 無理式の極限 受験の月




数列15 分母にルートがある形の数列の一般項 高2数学 数b Youtube




高校数学 数 13 ルート シリーズ 有理化編 Youtube




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



平方根 分母の有理化のやり方はこれでバッチリ 数スタ



数列で ルートが入った部分分数分解の問題なのですが 第k項は有理化して求める Yahoo 知恵袋




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




ルートの分数計算 問題解説で完全マスターだ 数スタ



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド




数学のルートの分数の二乗 この式の計算方法を教えてください 数学 教えて Goo




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ



1
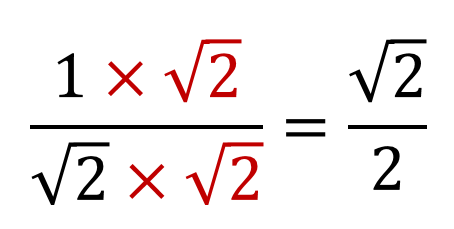



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




S計算 部分分数分解編 おいしい数学




平方根 ルート の重要な計算方法まとめ 数学fun




平方根 ルート の重要な計算方法まとめ 数学fun




複雑なルートの分数の有理化のやり方と問題 理系ラボ




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




分母の有理化の方法 数学の偏差値を上げて合格を目指す




高校数学 関数の極限の基本 3 問題編 映像授業のtry It トライイット




複素数の分数の実数化 分母の有理化の複素数版 Irohabook



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



ルート の分数計算教えてください すみません 急ぎです Yahoo 知恵袋




高校数学 繁分数式 分数の分数 の計算 受験の月




答えが分数のとき 分母にルートがあったら消す のように分母がマイナスのときはプラスに Clear




ルート分数の有理化 項2つ3つある場合は やり方まとめ 高校生 中学数学 理科の学習まとめサイト




ルートの入った計算なのですが この場合って分母に2をかけて分母を消してはダメですよね Clear




平方根 ルート の重要な計算方法まとめ 数学fun



1




有理化の計算 やり方は 分母のルートを分子にかけるだけ 中学や高校の数学の計算問題




数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




平方根 ルート の重要な計算方法まとめ 数学fun




実数 ルート を有理化する意味はこれでわかる 分母に がngの巻 Vol 9 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



Math 超簡単 有理化 分母に根号がない形にする 働きアリ



分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋




実数 ルート を有理化する意味はこれでわかる 分母に がngの巻 Vol 9 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校



この書き方は間違っていますか 分数とルートのときはルートを上に持ってい Yahoo 知恵袋




2の平方根 Wikipedia




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




ルートを分数にできない問題の背理法による証明 高校数学 Irohabook




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ



分数の2乗とは 1分でわかる意味 計算 書き方 との関係



分子と分母にルートがある分数式の変形 途中の分数の変形が何故こう Yahoo 知恵袋




中学数学 平方根 のコツ 有理化 加減乗除 展開




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




ルートを分数にできない問題の背理法による証明 高校数学 Irohabook
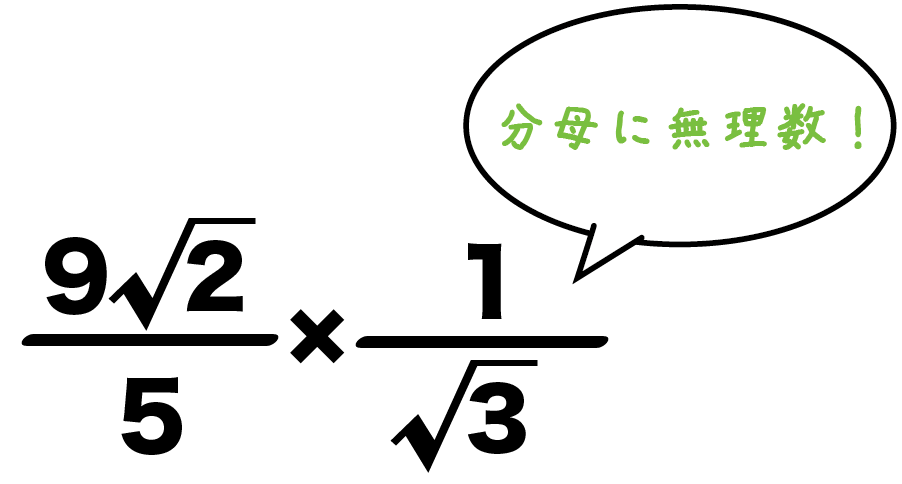



ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
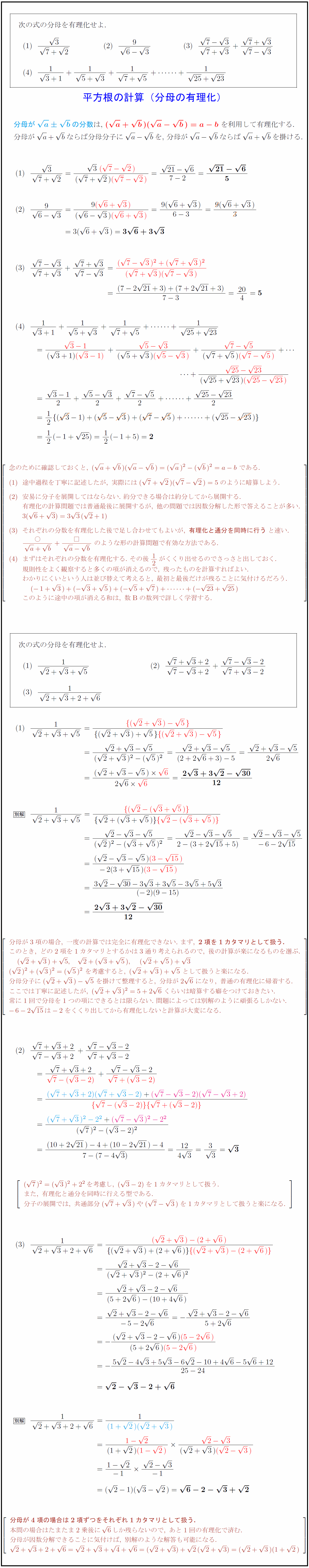



高校数学 平方根の計算 分母の有理化 受験の月
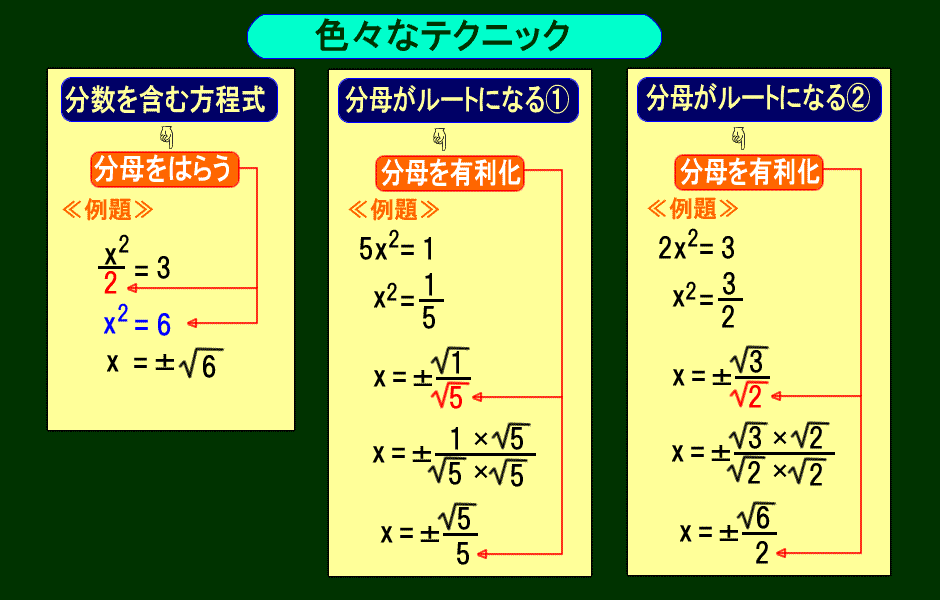



中学3年 数学 2次方程式 解き方 平方根の利用 有理化あり 問題1




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ
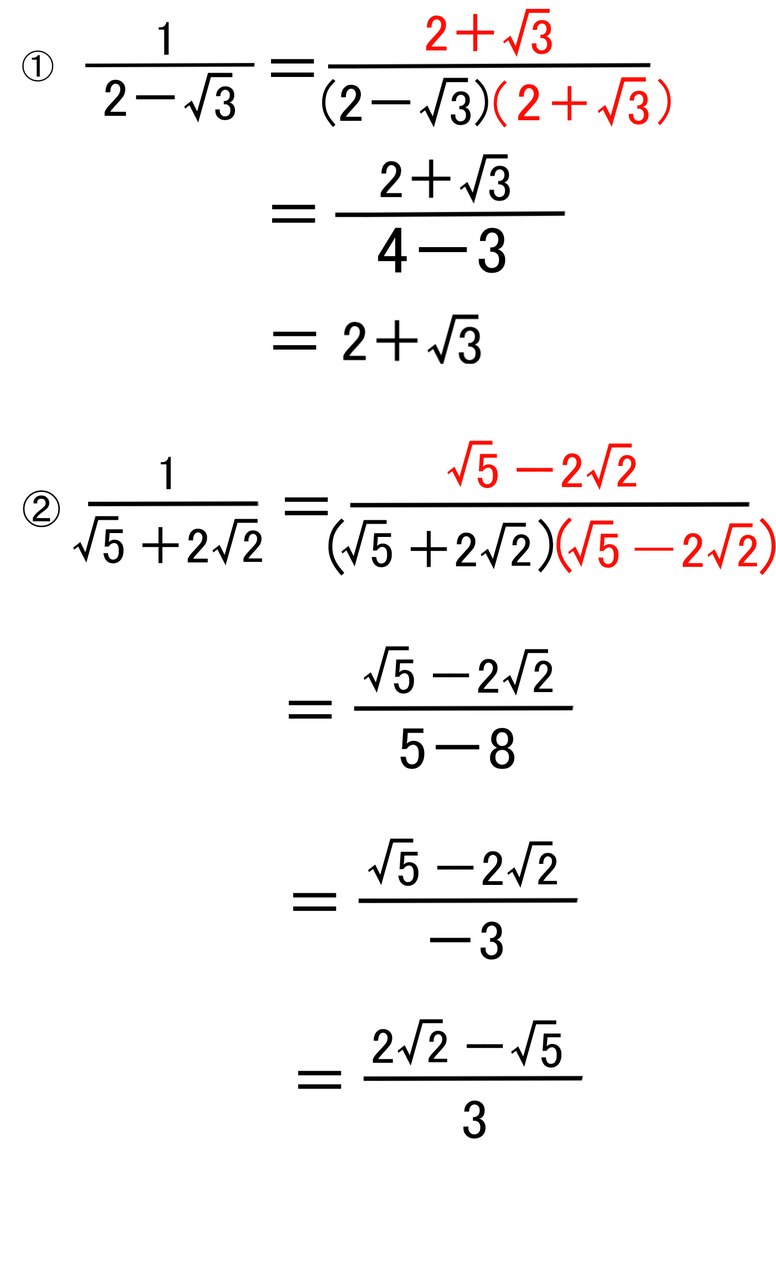



平方根 5 分母の有理化 バカでもわかる 中学数学




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題




文字の入った分数の約分とマイナスの扱い 分数の文字式の計算 Youtube




50 分数かける分数 やり方 最高のカラーリングのアイデア



分数関数の不定積分



分母にルートが使われている分数が入った計算方法がさっぱり分かりません Yahoo 知恵袋



Www Nhk Or Jp Kokokoza Library Tv Suugaku1 Archive Sugaku1 11 Pdf
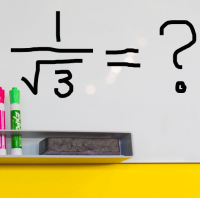



平方根 分母の根号 ルート をなくす 有理化 苦手な数学を簡単に




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ




分母の有理化 Youtube
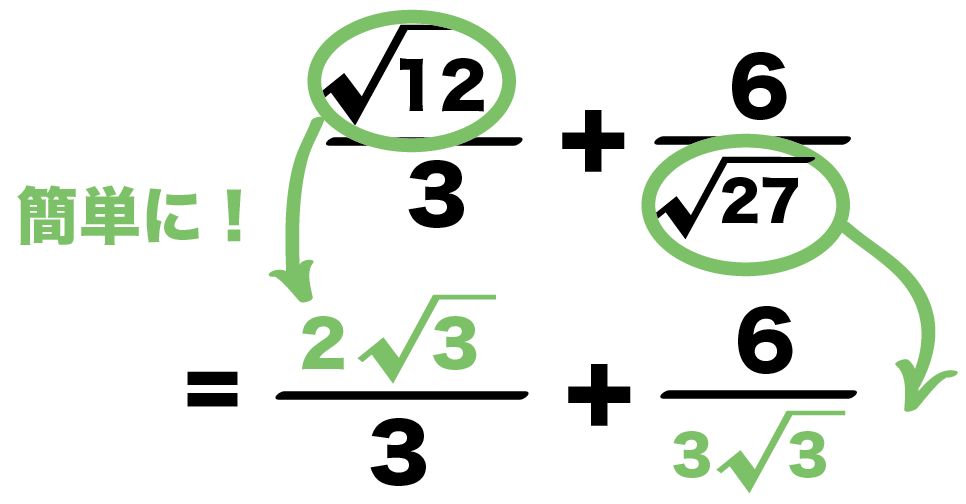



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




ルートの計算で分数の分母を有理化しないといけない理由とは さびねこ中学校




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




ルートの中を簡単にする と 分母の有理化 を比べる とちぎeライブラリ



0 件のコメント:
コメントを投稿